El desaf¨ªo de Dido de Tiro

EL PA?S y la Real Sociedad Matem¨¢tica Espa?ola plantean el segundo desaf¨ªo matem¨¢tico del verano. En esta ocasi¨®n, presenta el desaf¨ªo la doctora Mari Luz Garc¨ªa Escamilla, gestora del Posgrado en Matem¨¢ticas de la Universidad Aut¨®noma de Madrid.

Entre los acertantes se sortear¨¢ una colecci¨®n de libros Grandes Ideas de la Ciencia. Las soluciones deber¨¢n enviarse al correo electr¨®nico desafiodeagosto2@gmail.com antes de las 00.00 del martes 12 de agosto (medianoche del lunes al martes).

Para evitar errores y en atenci¨®n a nuestros lectores sordos, adem¨¢s del v¨ªdeo donde se plantea el desaf¨ªo, publicamos a continuaci¨®n el enunciado por escrito:

El poeta latino Virgilio cuenta en la Eneida como la princesa Dido de Tiro lleg¨® a la costa del norte de ?frica huyendo de su hermano el rey Pigmali¨®n. Al llegar le pidi¨® a Jarbas, rey de los g¨¦tulos, un terreno donde asentarse. Jarbas le contest¨® d¨¢ndole una piel de buey y comprometi¨¦ndose a regalarle toda la tierra que pudiera abarcar con ella.

Lo primero que hizo Dido fue mandar cortar la piel en una tira muy fina. Despu¨¦s pens¨® que abarcar¨ªa m¨¢s terreno si utilizaba, adem¨¢s de la cuerda fabricada con la piel de buey, la costa. As¨ª, colocando los extremos de la cuerda en la playa abarc¨® el terreno donde fund¨® despu¨¦s la ciudad de Cartago.

Nosotros vamos a presentar este mismo problema pero algo simplificado, ya que vamos a considerar que la costa que utiliz¨® Dido era una l¨ªnea recta. Con esta condici¨®n, la forma en la que hay que colocar la cuerda para abarcar la mayor superficie posible es una semicircunferencia con los extremos en la costa. Esta soluci¨®n, que se muestra en la figura de abajo a modo de ejemplo, la vamos a suponer conocida.

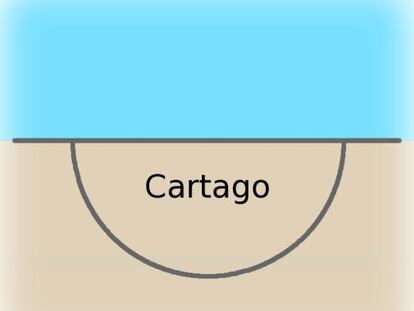
Y ahora, nuestro reto. El desaf¨ªo que proponemos esta semana consiste en calcular el ¨¢rea de la superficie m¨¢s grande que Dido puede abarcar con las siguientes condiciones:

1. La costa donde se va a establecer es un cabo formado por un ¨¢ngulo de 45 grados y dos lados rectos, como en esta figura:

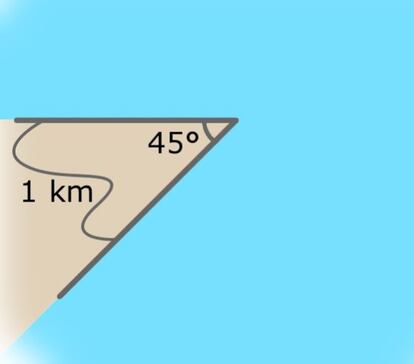
2. Dido ha conseguido sacar una cuerda de 1 kil¨®metro de longitud de la piel del buey.

Lo que pedimos es el valor del ¨¢rea de la superficie m¨¢xima que se puede formar con estas condiciones y una explicaci¨®n de por qu¨¦ no se puede hacer mejor.

?ADVERTENCIA: No se considerar¨¢n v¨¢lidas las respuestas en las que se utilicen derivadas, c¨¢lculo de variaciones, ni herramientas similares. S¨ª se puede usar, sin necesidad de justificar, la respuesta al problema simplificado comentada anteriormente como ejemplo.