El joven se lleva el torneo
El ganador del tercer desaf¨ªo matem¨¢tico del verano de EL PA?S es Carlos de Lorenzo, de Madrid
Manuel Abellanas, de la Universidad Polit¨¦cnica de Madrid, resuelve el tercer desaf¨ªo matem¨¢tico que este verano planteamos a nuestros lectores (puede ver aqu¨ª el v¨ªdeo). Una vez realizado el sorteo entre las respuestas correctas, de las 335 recibidas, el ganador de la colecci¨®n de libros Grandes Ideas de la Ciencia ha sido Carlos de Lorenzo, de Madrid.
Para evitar confusiones y en atenci¨®n tambi¨¦n a nuestros lectores sordos incluimos la soluci¨®n por escrito a continuaci¨®n:
La respuesta al reto que plante¨¢bamos es que ganar¨¢ el jugador m¨¢s joven. La raz¨®n es que, en las condiciones del desaf¨ªo, siempre se pueden dibujar 26 l¨ªneas y no m¨¢s. Por tanto, al participar cinco jugadores, tras cinco rondas, habr¨¢n dibujado 25 l¨ªneas y la ¨²ltima la dibujar¨¢ el jugador m¨¢s joven por ser quien comienza cada ronda.
Veamos por qu¨¦ es posible dibujar 26 l¨ªneas:
Denotemos L(P) al n¨²mero de l¨ªneas que se pueden dibujar con P puntos. Nuestro objetivo es ver que L(11)=26. Para ello empecemos analizando qu¨¦ pasar¨ªa si el n¨²mero de puntos es menor.
Si hay solo 4 puntos, la triangulaci¨®n ser¨¢ como esta

y, por tanto, L(4) = 5
Si hay 5 puntos, obtendremos una triangulaci¨®n como una de ¨¦stas
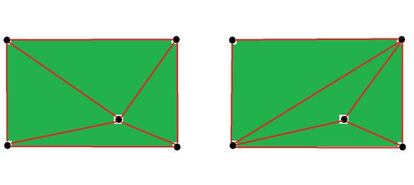
Y, por tanto, L(5) = 8.
Con 6 puntos se pueden obtener m¨¢s triangulaciones diferentes, pero observa que en todas ellas hay once l¨ªneas, por lo que L(6) = 11.
El n¨²mero de l¨ªneas que se obtienen para 4, 5, 6,¡ puntos es la sucesi¨®n 5, 8, 11, ¡ Ya se ve que cada vez que se a?ade otro punto, el n¨²mero de l¨ªneas aumenta tres unidades. Y, como el valor para cuatro puntos es cinco, resulta que el valor para P l¨ªneas es L(P) = 5+3(P-4), que es lo mismo que L(P)=3P-7. Esta f¨®rmula da el valor 26 para P = 11.
Solo nos falta demostrar que la f¨®rmula L(P) = 3P-7 se cumple para cualquier valor de P mayor que 4:
Como hemos visto, para 4, se cumple. Vamos a ver que si se cumple la f¨®rmula para un valor k mayor o igual que 4, entonces se cumple para el siguiente valor k+1. As¨ª se cumplir¨¢ para cualquier valor (incluido el 11 que es el que nos interesa).
Supongamos pues que la f¨®rmula se cumple para k puntos y supongamos que ahora tenemos k+1 puntos, k mayor o igual que 4.
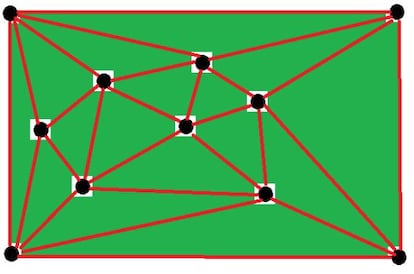
Si borramos uno de los puntos interiores y las l¨ªneas que salen de ¨¦l, nos quedar¨¢ un hueco en el dibujo con forma de pol¨ªgono.
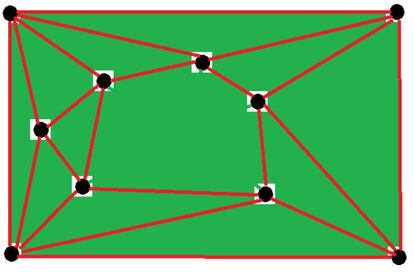
Si sal¨ªan del punto borrado m l¨ªneas, el hueco ser¨¢ un pol¨ªgono de m v¨¦rtices.
No es dif¨ªcil comprobar que un pol¨ªgono con m v¨¦rtices se descompone en tri¨¢ngulos (se triangula) dibujando m-3 de sus diagonales (en el ejemplo del dibujo el hueco tiene 5 v¨¦rtices y necesita 2 diagonales para ser triangulado).
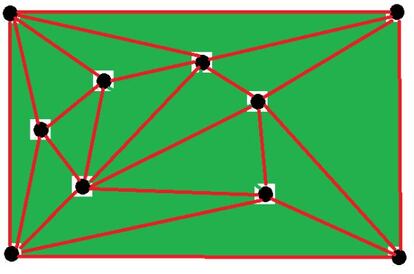
Triangulando el hueco que queda tras borrar el punto y las l¨ªneas que salen de ¨¦l, completamos una triangulaci¨®n de k puntos. Como estamos suponiendo que para k puntos la f¨®rmula se cumple, el n¨²mero de l¨ªneas que tendr¨¢ esta triangulaci¨®n es L(k)=3k-7. Pero, como hemos visto, el n¨²mero de l¨ªneas de la triangulaci¨®n de los k puntos es tres unidades menor que el de la triangulaci¨®n de los k+1 puntos (pues hab¨ªamos borrado m l¨ªneas y hemos tenido que a?adir solo m-3 para completar la triangulaci¨®n). Por tanto, el n¨²mero de l¨ªneas de la triangulaci¨®n original de los k+1 puntos debe ser 3k-7+3, es decir, 3(k+1)-7, que corresponde al valor de la f¨®rmula para P=k+1.
Bonito, ?verdad? De esta forma, no s¨®lo hemos obtenido el resultado para 11 puntos. Podemos saber el n¨²mero de l¨ªneas que habr¨¢ cuando juguemos con cualquier n¨²mero de puntos (mayor que 4, porque debe haber 4 en las esquinas).
Otras respuestas
Varios participantes han hecho el siguiente razonamiento geom¨¦trico elegante y sencillo: en cualquier triangulaci¨®n resultante al finalizar el juego, la suma de los ¨¢ngulos de los tri¨¢ngulos entorno a un punto interior es 360? y en los cuatro puntos de las esquinas suman 90?. En total la suma de todos los ¨¢ngulos de todos los tri¨¢ngulos es 7x360? + 4x90? = 2880?, que, dividido por 180? ¨C lo que suman los ¨¢ngulos de un tri¨¢ngulo cualquiera ¨C , da el n¨²mero de tri¨¢ngulos, 16, que tiene la triangulaci¨®n. Teniendo en cuenta que cada tri¨¢ngulo tiene tres lados y cada l¨ªnea de la triangulaci¨®n, salvo las cuatro del borde del rect¨¢ngulo, es compartida por dos tri¨¢ngulos, se obtiene que 3T+4 = 2L, siendo L el n¨²mero de l¨ªneas y T el de tri¨¢ngulos. En consecuencia L es 26 y por eso gana siempre el jugador que comienza la partida.
Los lectores m¨¢s matem¨¢ticos han empleado la conocida f¨®rmula de Euler que relaciona el n¨²mero de puntos con el de l¨ªneas y el de tri¨¢ngulos.
Cabe destacar que algunos participantes han empleado un m¨¦todo que, partiendo de cuatro puntos ¨C situados en las esquinas del campo ¨C los triangula con cinco l¨ªneas y a?ade los puntos interiores de uno en uno completando en cada paso una triangulaci¨®n del terreno de juego. Observan que bastan tres l¨ªneas para completar la triangulaci¨®n cada vez que se a?ade un punto interior. As¨ª se obtienen 26 l¨ªneas cuando se han a?adido todos los puntos. El m¨¦todo es correcto y demuestra que para cualquier posici¨®n de los puntos en las condiciones del problema hay una forma de terminar la partida con 26 l¨ªneas. Pero no queda probado que cualquier otra partida termine tambi¨¦n con 26 l¨ªneas. Las reglas del juego no exigen que los jugadores sigan necesariamente ese esquema al trazar las l¨ªneas y hay de hecho triangulaciones que no se pueden obtener de esa forma.
Tu suscripci¨®n se est¨¢ usando en otro dispositivo
?Quieres a?adir otro usuario a tu suscripci¨®n?
Si contin¨²as leyendo en este dispositivo, no se podr¨¢ leer en el otro.
FlechaTu suscripci¨®n se est¨¢ usando en otro dispositivo y solo puedes acceder a EL PA?S desde un dispositivo a la vez.
Si quieres compartir tu cuenta, cambia tu suscripci¨®n a la modalidad Premium, as¨ª podr¨¢s a?adir otro usuario. Cada uno acceder¨¢ con su propia cuenta de email, lo que os permitir¨¢ personalizar vuestra experiencia en EL PA?S.
En el caso de no saber qui¨¦n est¨¢ usando tu cuenta, te recomendamos cambiar tu contrase?a aqu¨ª.
Si decides continuar compartiendo tu cuenta, este mensaje se mostrar¨¢ en tu dispositivo y en el de la otra persona que est¨¢ usando tu cuenta de forma indefinida, afectando a tu experiencia de lectura. Puedes consultar aqu¨ª los t¨¦rminos y condiciones de la suscripci¨®n digital.

































































