Ajedrez y domin¨®

El ajedrez y el domin¨® son dos de los juegos de mesa m¨¢s populares y de mayor riqueza combinatoria: en el ajedrez, el n¨²mero de posibles posiciones compatibles con las reglas del juego es del orden de los septillones (?y en el domin¨®?). Y adem¨¢s de competir en popularidad y complejidad (y de ser especialmente adecuados para estos d¨ªas de confinamiento), el ajedrez y el domin¨® se prestan a interesantes consideraciones geom¨¦tricas y topol¨®gicas, como vimos la semana pasada.

En el ya cl¨¢sico problema del tablero mutilado (lo vi por primera vez, hace muchos a?os, en la maravillosa secci¨®n de juegos matem¨¢ticos de Martin Gardner, en Scientific American), es f¨¢cil ver que es imposible recubrirlo con 31 fichas de domin¨® si caemos en la cuenta de que, al quitar dos casillas del mismo color, quedar¨¢n 30 de un color y 32 del otro, y como cada ficha cubre una casilla blanca y otra negra, el recubrimiento pedido es imposible.

Antes de seguir con el ajedrez y el domin¨®, retomemos por un momento el juego de pares y nones en los mundos de Mickey y de los Simpson. Al tener sus personajes solo cuatro dedos, las posibles combinaciones en cada jugada son 5 x 5 = 25 (de 0-0 a 4-4); de estas 25 combinaciones, 12 dan suma impar y 13 par (el 0 se considera par), por lo que el que pide ¡°pares¡± tiene un 52 % de probabilidades de ganar frente al 48 % del que pide ¡°nones¡±.

Cubriendo el tablero

Volviendo al tablero de ajedrez y al domin¨®, nos pregunt¨¢bamos la semana pasada de cu¨¢ntas maneras distintas podemos recubrirlo con 32 fichas. Para abordar el problema, conviene empezar por tableros m¨¢s peque?os que el convencional de 8 x 8. Es evidente que el tablero de 2 x 2 solo se puede recubrir de una manera, con 2 fichas con sus lados mayores adyacentes; pero si tenemos en cuenta la orientaci¨®n de las fichas, las posibilidades son 2, ya que podemos colocarlas en horizontal o en vertical.

El tablero de 4 x 4 (el de 3 x 3 y los dem¨¢s de orden impar no pueden recubrirse con fichas de domin¨®, obviamente, ya que tienen un n¨²mero impar de casillas) admite 36 recubrimientos distintos, si tenemos en cuenta la orientaci¨®n, y el de 6 x 6, 6.728, seg¨²n ha calculado nuestro ¡°usuario destacado¡± Oli Lim¨®n (ver comentario 78 de la semana pasada). Por ¨²ltimo, en el tablero de 8 x 8 los posibles recubrimientos distintos son 12.988.816, casi 13 millones. Obs¨¦rvese lo r¨¢pidamente que crece la secuencia, cuyo siguiente t¨¦rmino (para un tablero de 10 x 10) es .258.584.046.368.

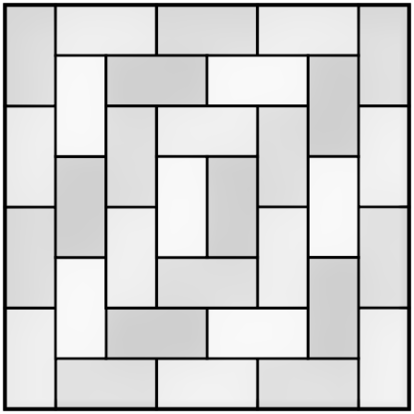
En la figura vemos uno de los posibles recubrimientos del tablero de 8 x 8 con 32 domin¨®s. ?Qu¨¦ peculiaridad tiene este recubrimiento concreto?

Si consideramos iguales los recubrimientos que solo se diferencian en la orientaci¨®n y, por tanto, coinciden al girar el tablero 90?, 180? o 270?, el n¨²mero disminuye considerablemente; en el caso trivial del tablero de 2 x 2, como hemos visto, se reduce a la mitad: de 2 posibilidades pasamos a 1. ?Y en el de 4 x 4, 6 x 6, 8 x 8¡­?

Y volviendo al tablero mutilado: si en vez de quitar las casillas de dos esquinas opuestas quitamos dos casillas de distinto color, ?podremos recubrirlo con 31 fichas? ?En qu¨¦ casos?

Carlo Frabetti es escritor y matem¨¢tico, miembro de la Academia de Ciencias de Nueva York. Ha publicado m¨¢s de 50 obras de divulgaci¨®n cient¨ªfica para adultos, ni?os y j¨®venes, entre ellos Maldita f¨ªsica, Malditas matem¨¢ticas o El gran juego. Fue guionista de La bola de cristal.

Puedes seguir a Materia en Facebook, Twitter, Instagram o suscribirte aqu¨ª a nuestra newsletter.