Poliomin¨®s

El pentomin¨® F, como se apunt¨® la semana pasada, es el ¡°oscilador¡± R en el juego de la vida de Conway. Un oscilador es un patr¨®n que se autorreproduce tras un cierto n¨²mero de jugadas (o ¡°generaciones¡± en la jerga del juego). El oscilador R no es en absoluto evidente, pues necesita nada menos que 1.103 generaciones para volver a su forma original, y en el proceso genera cientos de ¡°naves espaciales¡± y otros patrones intermedios.

?Qu¨¦ otros pentomin¨®s, tetromin¨®s o tromin¨®s son patrones destacados en el juego de la vida?

Es f¨¢cil encontrar en la red las soluciones a los rompecabezas con pentonim¨®s planteados la semana pasada, por lo no voy a spoilear a quienes quieran seguir intent¨¢ndolo, e insisto en la conveniencia de adquirir un juego de pentomin¨®s en cualquier tienda especializada.

Una gran familia de poliformas

Del mismo modo que los tri¨¢ngulos, los cuadril¨¢teros y los pent¨¢gonos son pol¨ªgonos de tres, cuatro y cinco lados respectivamente, los tromin¨®s, tetromin¨®s y pentomin¨®s, de los que nos hemos ocupado en las ¨²ltimas semanas, son poliomin¨®s de tres, cuatro y cinco cuadrados adyacentes.

Los poliomin¨®s fueron denominados as¨ª y estudiados sistem¨¢ticamente, a partir de los a?os cincuenta del siglo pasado, por el matem¨¢tico e ingeniero estadounidense Solomon W. Golomb, que, adem¨¢s de su inter¨¦s por los juegos matem¨¢ticos, es conocido por sus importantes aportaciones a la teor¨ªa de codificaci¨®n. Y, una vez m¨¢s, fue Martin Gardner quien populariz¨® los poliomin¨®s en su secci¨®n de juegos matem¨¢ticos de Scientific American.

Como ya hemos podido empezar a ver en semanas anteriores, a medida que aumenta el n¨²mero de cuadrados de los poliomin¨®s se incrementa r¨¢pidamente el n¨²mero de formas distintas posibles. Solo hay 2 tromin¨®s libres, 5 tetromin¨®s, 12 pentomin¨®s y 35 hexomin¨®s. ?Cu¨¢ntos hexomin¨®s no libres hay? ?Y heptomin¨®s libres y no libres? ?Sigue alguna pauta la secuencia los n¨²meros de poliomin¨®s a medida que aumenta el n¨²mero de cuadrados?

Inciso: Los poliomin¨®s ¡°no libres¡± se denominan ¡°unilaterales¡± (pues tambi¨¦n se cuentan los obtenidos por simetr¨ªa especular), y si no se especifica lo contrario, y puesto que los poliomin¨®s se suelen utilizar como piezas f¨ªsicas de rompecabezas, se sobreentiende que se habla de los libres. Por la misma raz¨®n, en ocasiones no se tienen en cuenta los poliomin¨®s ¡°con agujeros¡±, que, como veremos acto seguido, aparecen a partir de los heptomin¨®s. Fin del inciso.

Vimos que con los 12 pentomin¨®s se pueden formar rect¨¢ngulos de 6 x 10, 5 x 12, 4 x 15 y 3 x 20. ?Se puede formar alg¨²n rect¨¢ngulo con los 35 hexomin¨®s?

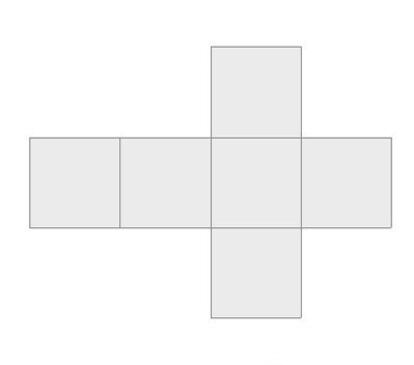
El consabido desarrollo plano del cubo en forma de cruz es un hexomin¨®. ?Hay otros hexomin¨®s que tambi¨¦n son posibles desarrollos planos del cubo? ?Cu¨¢ntos y cu¨¢les son?

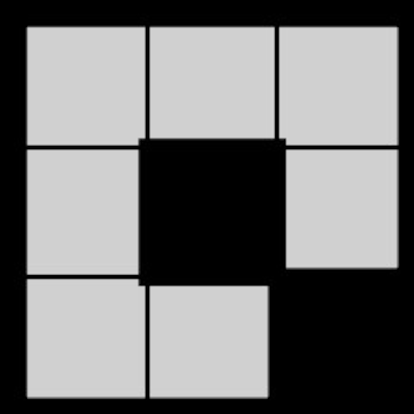
Con los heptomin¨®s se inaugura un tipo de poliomin¨® que no existe en los casos anteriores: el poliomin¨® con agujeros. Solo hay un heptomin¨® con agujero, pero entre los octomin¨®s hay varios. ?Cu¨¢ntos y cu¨¢les?

Carlo Frabetti es escritor y matem¨¢tico, miembro de la Academia de Ciencias de Nueva York. Ha publicado m¨¢s de 50 obras de divulgaci¨®n cient¨ªfica para adultos, ni?os y j¨®venes, entre ellos ¡®Maldita f¨ªsica¡¯, ¡®Malditas matem¨¢ticas¡¯ o ¡®El gran juego¡¯. Fue guionista de ¡®La bola de cristal¡¯.

Puedes seguir a Materia en Facebook, Twitter, Instagram o suscribirte aqu¨ª a nuestra newsletter