Caminos de celos¨ªa

?Cu¨¢l es el quinto n¨²mero de Motzkin?, nos pregunt¨¢bamos la semana pasada. He aqu¨ª la respuesta de Manuel Amor¨®s: ¡°Vamos a razonar para obtener de forma recursiva M(5), el n¨²mero de Motzkin para 5 puntos. Consideremos un v¨¦rtice determinado V. Pueden pasar dos cosas: desde ese v¨¦rtice sale alguna cuerda o no sale ninguna. En el segundo caso dicho v¨¦rtice no interviene en las formas de unir los cuatro puntos que quedan, y por tanto tenemos M(4) opciones. Si una cuerda sale de V dividir¨¢ el c¨ªrculo en dos partes independientes, ya que no podemos atravesarla. Podemos combinar las posibilidades a ambos lados, que son a su vez n¨²meros de Motzkin, donde se descuentan los dos v¨¦rtices de la cuerda separatoria. Resumiendo: M(5) = M(4) + M(0)*M(3) + M(1)*M(2) + M(2)*M(1) + M(3)*M(0). Sustituyendo los valores conocidos M(0) = 1, M(1) = 1, M(2) = 2, M(3) = 4, M(4) = 9, obtenemos: M(5) = 9 + 4 +2 + 2 + 4 = 21¡å.

Al igual que ocurre con los n¨²meros de Delannoy, no hay una f¨®rmula sencilla que d¨¦ M(n) en funci¨®n de n, hay que utilizar sumatorios o integrales (o hallarlos por recurrencia, como acabamos de ver).

En cuanto a la relaci¨®n de los n¨²meros de Motzkin con los de Delannoy, tiene que ver con los posibles recorridos efectuados en una cuadr¨ªcula de acuerdo con ciertas reglas, es decir, con los denominados gen¨¦ricamente ¡°caminos de celos¨ªa¡± (lattice paths en ingl¨¦s).

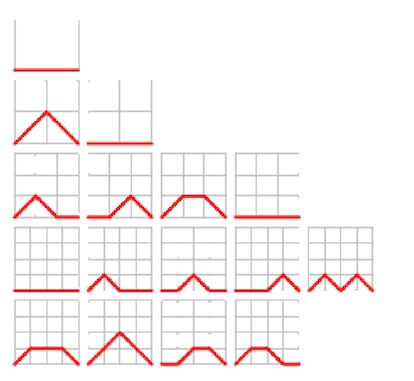
?De cu¨¢ntas maneras distintas podemos ir del v¨¦rtice inferior izquierdo al v¨¦rtice inferior derecho de una cuadr¨ªcula de n x n en n pasos, si los pasos son lados o diagonales de las casillas?

En la figura vemos las distintas posibilidades para las cuadr¨ªculas de 1 x 1 (1 camino), 2 x 2 (2 caminos), 3 x 3 (4 caminos) y 4 x 4 (9 caminos). Y, s¨ª, son los n¨²meros de Motzkin, definidos de una manera distinta a como lo hicimos anteriormente y muy similar a como se definen los n¨²meros de Delannoy: ambos tipos de n¨²meros son variantes de los caminos de celos¨ªa.

A este respecto, comenta Bretos Burs¨®: ¡°No s¨¦ ver la relaci¨®n que sugiere Carlo entre los n¨²meros (o caminos) de Delannoy y los de Motzkin, pero s¨¦ una forma bonita de sacar los n¨²meros de Motzkin. En el tri¨¢ngulo de arriba cada n¨²mero es suma del que tiene encima y el que tiene encima a la izquierda (es el de Pascal, claro). En el de abajo, cada n¨²mero es suma de los que tiene encima, encima a la derecha y encima a la izquierda, y la primera columna es la de los n¨²meros de Motzkin¡±.

N¨²meros de Narayana

No se puede hablar de los n¨²meros de Delannoy y los de Motzkin sin mencionar los de Narayana (denominados as¨ª en honor del matem¨¢tico canadiense de origen indio T. V. Narayana). Al igual que los de Delannoy, un n¨²mero de Narayana se define en funci¨®n de dos naturales: N(m, n), donde n es menor o igual a m.

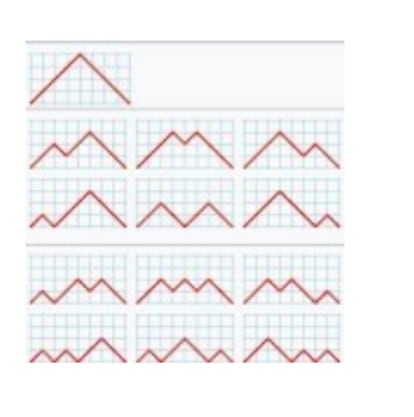
Y al igual que los de Delannoy y los de Motzkin, los n¨²meros de Narayana representan los distintos caminos posibles que permiten recorrer una cuadr¨ªcula de acuerdo con determinadas reglas. Sabiendo que en la figura est¨¢n representados los n¨²meros de Narayana N(4, 1) = 1, N(4, 2) = 6 y N(4, 3) = 6, ?puedes hallar N(4, 4)?

Por cierto, no hay que confundir a T. V. Narayana (1930-1987) con Narayana Pandita (1340-1400), otro ilustre matem¨¢tico indio famoso por el problema de las vacas de Narayana, parientes cercanas de los conejos de Fibonacci. Pero ese es otro art¨ªculo.

Puedes seguir a MATERIA en Facebook, Twitter e Instagram, o apuntarte aqu¨ª para recibir nuestra newsletter semanal.