La torre, el cubo y el tablero

EL PA?S y Materia proponen a sus lectores, cada semana, un juego de l¨®gica. Los lectores pueden enviar sus soluciones en los comentarios, y plantear nuevos acertijos y juegos. La respuesta correcta ser¨¢ ofrecida en la columna de la semana siguiente.

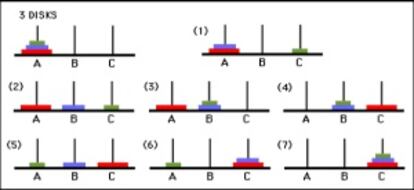
Para hallar la secuencia de movimientos necesarios para trasladar los discos de un eje a otro en la torre de Han¨®i de tres discos de la semana anterior, partamos del caso m¨¢s sencillo posible: una torre trivial de un solo disco, en la que es evidente que basta un movimiento para trasladar ese disco a otro eje. Una torre de dos discos tambi¨¦n es trivial: trasladamos el menor a uno de los dos ejes libres, el mayor al otro eje libre, y por ¨²ltimo ponemos el menor sobre el mayor. Consideremos ahora nuestra torre de tres discos, que numeraremos de menor a mayor: 1, 2 y 3. Para el primer movimiento solo hay una opci¨®n: trasladar el disco 1 a uno de los dos ejes libres. Para el segundo movimiento solo hay una opci¨®n no repetitiva: pasar el disco 2 al eje libre. Los siguientes movimientos no son ¨²nicos, pero s¨ª bastante obvios: 3?) 1 sobre 2, 4?) 3 al eje libre, 5?) 1 al eje libre, 6?) 2 sobre 3, 7?) 1 sobre 2. La secuencia es, pues, 1213121.

Como vimos, William Hamilton estudi¨® en todos los s¨®lidos plat¨®nicos, y no solo en el dodecaedro, los recorridos que llevan su nombre. En el caso de un cubo, si llamamos 1 a la direcci¨®n vertical, 2 a la horizontal y 3 a la anteroposterior, partiendo, por ejemplo, del v¨¦rtice A del cubo de la figura y efectuando el sencillo recorrido hamiltoniano AEFBCGHD, que pasa por todos los v¨¦rtices una sola vez, vemos que la secuencia direccional (y dimensional) del ciclo es 1213121, la misma que en una torre de Han¨®i de tres discos.

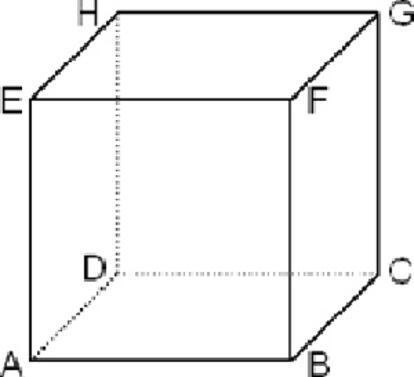
Y, como tambi¨¦n vimos la semana pasada, a mediados del siglo pasado D. W. Crowe demostr¨® que este sorprendente isomorfismo se mantiene para torres de cualquier altura y cubos de cualesquiera dimensiones: el orden en el que hay que mover n discos de una torre de Han¨®i para trasladarlos a otro eje, se corresponde exactamente con la secuencia direccional (y dimensional) de un recorrido hamiltoniano en un cubo de n dimensiones.

Por otra parte, y como es bien sabido, el m¨ªtico inventor del ajedrez le pidi¨® al rey de la India un grano de trigo por la primera casilla del tablero, dos por la segunda, cuatro por la tercera, ocho por la cuarta, y as¨ª sucesivamente hasta la casilla 64, doblando en cada una el n¨²mero de granos de trigo de la anterior. Pues bien, este n¨²mero astron¨®mico (18.446.744.073.709.551.615) es igual al n¨²mero de traslados necesarios para pasar de un eje a otro los 64 discos de oro de la torre de Brahma (y tambi¨¦n, como acabamos de ver, al n¨²mero de aristas que hay que recorrer en un hipercubo de 64 dimensiones para efectuar un ciclo hamiltoniano).

?C¨®mo se explica la sorprendente equivalencia?

Carlo Frabetti

Escritor y matem¨¢tico, miembro de la Academia de Ciencias de Nueva York, ha publicado m¨¢s de 50 obras de divulgaci¨®n cient¨ªfica para adultos, ni?os y j¨®venes, entre ellos ¡®Maldita f¨ªsica¡¯, ¡®Malditas matem¨¢ticas¡¯ o ¡®El gran juego¡¯. Fue guionista de ¡®La bola de cristal¡¯