El problema de las ocho damas

El problema de las ocho damas, propuesto la semana pasada, fue planteado por primera vez por el ajedrecista alem¨¢n Max Bezzel, que, con el seud¨®nimo Schachfreund, lo public¨® en 1848 en la revista especializada Berliner Schachzeitung. Puesto que la dama puede desplazarse horizontal, vertical o diagonalmente, el problema equivale a situar ocho fichas en el tablero de forma que no haya dos en la misma fila, columna o diagonal (lo cual lo emparenta con el popular sudoku).

El problema de las ocho damas fue analizado, entre otros, por el mism¨ªsimo Gauss, que hall¨® 76 de las 92 soluciones posibles; pero el primero en encontrarlas todas, en 1850, fue un amigo suyo, el matem¨¢tico ciego Franz Nauck.

En realidad, solo hay 12 soluciones b¨¢sicas, y las 80 restantes se obtienen por giros y simetr¨ªas; 11 de las soluciones b¨¢sicas valen por 8: girando cualquiera de ellas 90?, 180? y 270? se obtienen tres m¨¢s, y las cuatro dan lugar a otras cuatro por simetr¨ªa especular; pero la duod¨¦cima (damas en a3, b5, c2, d8, e1, f7, g4 y h6) solo vale por cuatro, pues tiene simetr¨ªa central. Las 12 soluciones b¨¢sicas dan, pues, lugar a 11 x 8 + 4 = 92 soluciones distintas.

Puesto que solo puede haber una dama por columna, podemos expresar num¨¦ricamente las soluciones anotando, de izquierda a derecha, los n¨²meros de las filas que ocupan. As¨ª, la soluci¨®n sim¨¦trica que acabamos de ver ser¨ªa 35281746. El problema de las ocho damas se puede convertir, de este modo, en un problema aritm¨¦tico, que consiste en tomar, de entre todas las permutaciones de los d¨ªgitos del 1 al 8, las que cumplen cierta condici¨®n. Sin embargo, esta notaci¨®n num¨¦rica no es de gran ayuda, salvo para realizar un programa de b¨²squeda por ordenador, pues las permutaciones de los ocho d¨ªgitos son 8! = 8 x 7 x 6 x 5 x 4 x 3 x 2 x 1 = 40.320, entre las cuales hay que buscar las 92 que cumplen la condici¨®n requerida. Por cierto, ?qu¨¦ condici¨®n es esa?

M¨¢s dif¨ªcil todav¨ªa, ?hay alguna soluci¨®n en la que no haya ning¨²n grupo de tres damas alineadas? ?Cu¨¢l es -si existe- su notaci¨®n num¨¦rica?

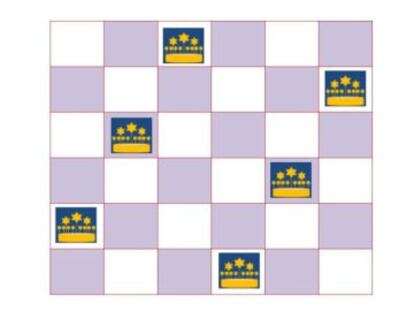
Solo hay una soluci¨®n b¨¢sica para el tablero de 4 x 4 y otra para el de 6 x 6, y dos para el de 5 x 5, que en la notaci¨®n num¨¦rica antes establecida ser¨ªan, respectivamente, 2413, 246135, 25314 y 35241; las tres primeras tienen simetr¨ªa central.

Problemas afines

?Cu¨¢ntas damas son necesarias, como m¨ªnimo, para cubrir todo el tablero? Por cubrir o abarcar el tablero se entiende que todas las casillas est¨¦n a tiro de alguna de las damas.

?Y para abarcar tableros de 9 x 9, 10 x 10 y 11 x 11?

?Cu¨¢ntas torres podemos colocar en el tablero de forma que ninguna amenace a ninguna otra? ?De cu¨¢ntas maneras distintas podemos colocarlas?

Carlo Frabetti es escritor y matem¨¢tico, miembro de la Academia de Ciencias de Nueva York. Ha publicado m¨¢s de 50 obras de divulgaci¨®n cient¨ªfica para adultos, ni?os y j¨®venes, entre ellos ¡®Maldita f¨ªsica¡¯, ¡®Malditas matem¨¢ticas¡¯ o ¡®El gran juego¡¯. Fue guionista de ¡®La bola de cristal¡¯