La paradoja de Bertrand: tri¨¢ngulos, circunferencias y probabilidad

Como ya sab¨¦is los lectores de El Aleph, me encantan los tri¨¢ngulos, por lo que no me he podido resistir a hablaros de una curiosa paradoja relacionada con ellos de la cual tuve conocimiento hace ya unos a?os.

El tema que nos ocupa trata sobre circunferencias, tri¨¢ngulos y probabilidad. Y, por lo que parece, estos tres ingredientes forman una mezcla explosiva, matem¨¢ticamente hablando. Vamos a plantear la cuesti¨®n y despu¨¦s indagaremos en las posibles soluciones.

El enunciado de nuestro problema es el siguiente:

¡°Tomamos una circunferencia e inscribimos en ella un tri¨¢ngulo equil¨¢tero (tri¨¢ngulo con los tres lados y los tres ¨¢ngulos iguales). Escogemos ahora una cuerda al azar (una cuerda es cualquier segmento que une dos puntos de la circunferencia). ?Cu¨¢l es la probabilidad de que la longitud de dicha cuerda sea mayor que la longitud del lado del tri¨¢ngulo?¡±

En la imagen siguiente pod¨¦is ver un tri¨¢ngulo equil¨¢tero inscrito en una circunferencia y cuerdas de distintas longitudes:

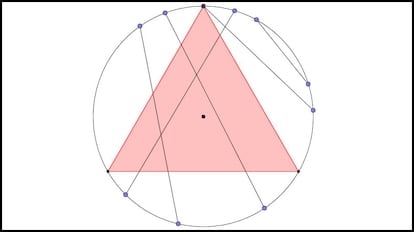
Este problema se conoce con el sugerente nombre de la paradoja de Bertrand, debido a que fue el matem¨¢tico franc¨¦s Joseph Bertrand quien la introdujo en su libro Calcul des probabilit¨¦s en 1889. Que se le califique como una paradoja se va a entender enseguida.

Adentr¨¦monos en la soluci¨®n. Tomamos un punto cualquiera de la circunferencia, el que queramos. Como la posici¨®n en la que dibujemos el tri¨¢ngulo es indiferente, podemos hacer coincidir dicho punto con uno de sus v¨¦rtices, digamos que el superior en la imagen anterior. Si ahora trazamos una cuerda, elegida al azar, desde ese v¨¦rtice, puede ser que la cuerda llegue al arco de circunferencia inferior, con lo que la cuerda ser¨ªa mayor que el lado del tri¨¢ngulo. Pero tambi¨¦n puede ser que llegue a alguno de los dos arcos laterales, y entonces la cuerda ser¨ªa menor que el lado. Ambas opciones est¨¢n representadas en la imagen:

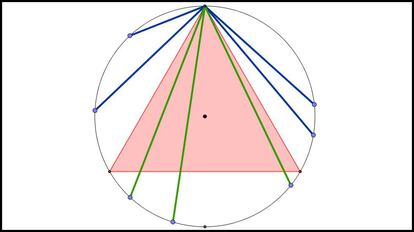
Como nuestro tri¨¢ngulo es equil¨¢tero, los tres arcos son iguales. Y como dos de los arcos dan cuerdas menores y uno da cuerdas mayores, la probabilidad de que la cuerda sea mayor que el lado del tri¨¢ngulo es 1/3.

Cuesti¨®n solucionada, ?verdad? Pues la cosa es que no. Veamos el problema de la siguiente forma: tomemos un radio cualquiera del c¨ªrculo y giremos el tri¨¢ngulo hasta que uno de los lados sea perpendicular a dicho radio. La cuerda la trazamos escogiendo al azar un punto de dicho radio y trazando la cuerda que pasa por dicho punto y es perpendicular al radio, como aparece en la imagen:

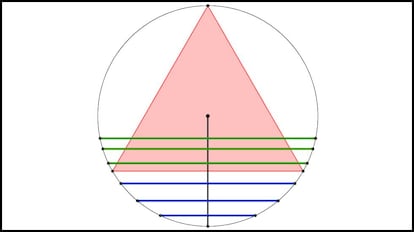
Como se puede ver, la cuerda es mayor que el lado del tri¨¢ngulo si pasa por un punto de la parte interior del radio, y menor que el lado si pasa por un punto de la otra parte del mismo. Como el lado del tri¨¢ngulo divide al radio en dos partes iguales, se tiene que la probabilidad de que la cuerda sea mayor que el lado del tri¨¢ngulo es 1/2.

Vaya, pues parece que la cosa no es tan sencilla como pod¨ªa parecer. Y lo peor (o lo mejor) es que a¨²n hay m¨¢s.

Tomemos ahora un punto al azar dentro del c¨ªrculo, y tracemos la cuerda que tiene a ese punto como punto medio. Si dibujamos ahora el c¨ªrculo inscrito en el tri¨¢ngulo (que tiene de radio la mitad que el radio del c¨ªrculo inicial), se tiene que si el punto escogido cae dentro de este c¨ªrculo inscrito, entonces la cuerda es mayor que el lado de nuestro tri¨¢ngulo; y que si el punto est¨¢ fuera de dicho c¨ªrculo inscrito, entonces la cuerda es menor que el lado. Pod¨¦is verlo en la siguiente imagen:

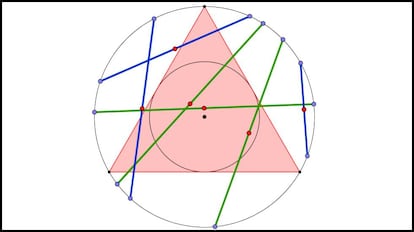
Calculamos entonces la probabilidad dividiendo el ¨¢rea favorable, la del c¨ªrculo inscrito, entre el ¨¢rea total, la del c¨ªrculo inicial. Si R es el radio del c¨ªrculo inicial, tenemos que el ¨¢rea total es ¦ÐR² y que el ¨¢rea del c¨ªrculo inscrito es ¦Ð(R/2)². Realizando la divisi¨®n correspondiente tenemos que la probabilidad de que la cuerda sea mayor que el lado del tri¨¢ngulo es 1/4.

Recapitulando, tenemos un problema de probabilidad con tres soluciones distintas, hecho que choca frontalmente con la propia concepci¨®n de probabilidad. ?Qu¨¦ ocurre? La soluci¨®n cl¨¢sica es que necesitamos definir claramente qu¨¦ entendemos por elegir una cuerda al azar. En el momento en que la elecci¨®n al azar est¨¦ bien definida, podremos responder a la pregunta que nos plantean.

Pero claro, esta soluci¨®n se queda algo corta. Y no soy el ¨²nico que lo piensa, ya que, a pesar de que el problema se plante¨® y se trat¨® hace m¨¢s de 100 a?os, han sido varios los matem¨¢ticos que se han interesado por ¨¦l y que han publicado trabajos al respecto.

Uno de los que me parecen m¨¢s interesantes es el de Edwin Jaynes, que en 1973 public¨®?The Well-Posed Problem. En dicho trabajo comenta que en este problema deber¨ªa aplicarse el llamado principio de m¨¢xima ignorancia, que en nuestro caso implica que el problema deber¨ªa ser invariante frente a cambios de escala y traslaciones de la circunferencia inicial. Esto es, si tomamos circunferencias menores o trasladadas, la distribuci¨®n de las cuerdas deber¨ªa ser igual a la que hay en la circunferencia inicial. Analizando las distribuciones de las cuerdas de los tres m¨¦todos (im¨¢genes tomadas de aqu¨ª):

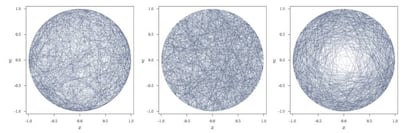
se llega a la conclusi¨®n de que el ¨²nico m¨¦todo que mantiene invariantes la escala y la traslaci¨®n es el m¨¦todo 2.

Pero Jaynes no ha sido el ¨²nico que se ha interesado por la paradoja de Bertrand en los ¨²ltimos a?os. En 2014, Diederik Aerts y Massimiliano Sassoli de Bianchi publicaron Solving the Hard Problem of Bertrand¡¯s Paradox, en el que, mediante un nuevo enfoque, acaban llegando a unos resultados num¨¦ricos que est¨¢n de acuerdo con los resultado de Jaynes.

?Resuelve esto nuestra paradoja? Pues la verdad es que no est¨¢ demasiado claro. Parece que en los ¨²ltimos tiempos muchos coinciden en que el m¨¦todo 2 ser¨ªa el m¨¢s aconsejable, pero, al menos yo, no encuentro razones suficientes para desechar los otros dos m¨¦todos. Y tampoco para que, visto lo visto, pudiera existir alg¨²n otro m¨¦todo que arrojara un resultado distinto. ?Qu¨¦ os parece a vosotros?