Los tesoros matem¨¢ticos que esconde el tri¨¢ngulo de Pascal

Cuando uno escucha la palabra tri¨¢ngulo, la primera imagen que le viene a la cabeza es la misma, la que seguramente tendr¨¦is ahora mismo en vuestra mente. Pero el tema que nos ocupa hoy no va exactamente de ese tipo de tri¨¢ngulos, sino de un tri¨¢ngulo num¨¦rico, una cierta disposici¨®n de n¨²meros en forma de tri¨¢ngulo.

El tri¨¢ngulo de Pascal (o tri¨¢ngulo de Tartaglia) est¨¢ formado por infinitas filas de n¨²meros, y se construyen de la siguiente forma:

- La primera fila, la Fila 0, tiene solamente un uno: 1.

- La segunda, la Fila 1, tiene dos unos, a izquierda y derecha del uno anterior: 1 1

- La tercera fila, la Fila 2, se construye as¨ª: sumamos los dos n¨²meros de la anterior y colocamos el resultado, 2, debajo del hueco que dejan dichos n¨²meros, y a izquierda y derecha colocamos dos unos. Nos queda as¨ª: 1 2 1.

- La cuarta fila, y las posteriores, se construyen del estilo a la tercera: debajo de cada hueco entre dos n¨²meros de la fila anterior escribimos la suma de dichos n¨²meros, y a izquierda y derecha colocamos dos unos. Por ejemplo, la Fila 3 quedar¨ªa as¨ª: 1 3 3 1. Y la Fila 4 as¨ª: 1 4 6 4 1. En la siguiente imagen pod¨¦is ver las primeras nueve filas del tri¨¢ngulo de Pascal:

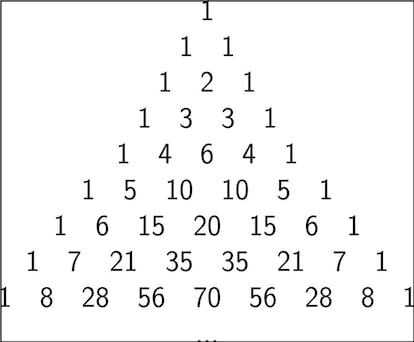
Su nombre se debe al matem¨¢tico franc¨¦s Blaise Pascal (y el otro al matem¨¢tico italiano Niccolo Fontana, apodado Tartaglia por su condici¨®n de tartamudo), aunque parece que este objeto matem¨¢tico ya era conocido en la antigua China.

Bonito, ?verdad? Bien, pues en lo que nos queda de art¨ªculo vamos a ver unas cuantas interesantes propiedades de este tri¨¢ngulo num¨¦rico, algunas de ellas muy populares y otras no tan conocidas y ciertamente curiosas.

Lo primero que vamos a explicar es el porqu¨¦ de llamar Fila 0 a la primera fila, Fila 1 a la segunda, y as¨ª sucesivamente. Una raz¨®n podr¨ªa ser la siguiente: si sumamos los n¨²meros de la Fila n, el resultado es exactamente 2ⁿ: la suma de los de la Fila 0 es 1, que es 2⁰, los de la Fila 1 suman 2, que es 2¹, los de la Fila 2 suman 4, que es 2², etc:

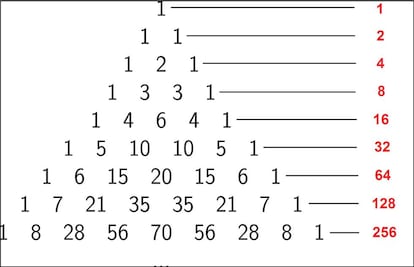
Pero podr¨ªamos dar otra raz¨®n: los n¨²meros de la Fila n son los coeficientes del desarrollo del binomio (a+b)ⁿ. Lo vemos:

- (a+b)⁰=1

- (a+b)¹=1 ¡¤ a + 1 ¡¤ b

- (a+b)²=1 ¡¤ a² + 2 ¡¤ ab + 1 ¡¤ b²

- (a+b)³=1 ¡¤ a³ + 3 ¡¤ a²b + 3 ¡¤ ab² + 1 ¡¤ b³

Veamos ahora algunos objetos matem¨¢ticos que podemos encontrar de manera sencilla en el tri¨¢ngulo de Pascal. Por ejemplo, es sencillo encontrar en ¨¦l los n¨²meros naturales: est¨¢n en la diagonal recuadrada de la imagen de la izquierda. Y tambi¨¦n es f¨¢cil encontrar los n¨²meros triangulares: aparecen en la diagonal recuadrada en la imagen de la derecha:

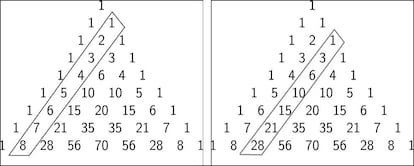
Un pel¨ªn m¨¢s escondidos, pero no demasiado, est¨¢n los n¨²meros cuadrados: 1, 4, 9, 16, 25, etc. Est¨¢n en la misma diagonal de los triangulares, sumando cada dos consecutivos:

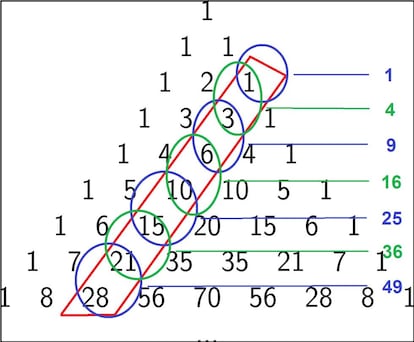
Otra curiosidad num¨¦rica es que si el segundo n¨²mero de una fila es primo, entonces el resto de n¨²meros de esa fila (salvo los unos de los extremos) son m¨²ltiplos de dicho n¨²mero primo. Por ejemplo, en la Fila 6, el segundo n¨²mero, 5, es primo, y el resto, 10, es m¨²ltiplo de 5; y en la Fila 8, el segundo n¨²mero, 7, es primo, y el resto, 21 y 35, son ambos m¨²ltiplos de 7. Pod¨¦is generar vosotros mismos m¨¢s filas del tri¨¢ngulo y comprobar que esta propiedad se cumple siempre.

Y una m¨¢s relacionada directamente con las filas: si tomamos cada fila como un n¨²mero, tenemos las potencias de 11. La Fila 0, 1, es 11⁰, la Fila 1, 11, es 11¹, la Fila 2, 121, es 11², y as¨ª sucesivamente¡­ Un momento, ?qu¨¦ ocurre, por ejemplo, con la Fila 5, 1-5-10-10-5-1? Pues que, realizando la siguiente operaci¨®n

1-(5+1)-(0+1)-0-5-1

Obtenemos el n¨²mero 161051, que es 11⁵. Pod¨¦is comprobar que con el resto de filas ocurre lo mismo.

La siguiente propiedad curiosa de este tri¨¢ngulo de Pascal es el llamado stick de Hockey: si comenz¨¢is en un 1 cualquiera y vais en diagonal, la suma de todos los n¨²meros recorridos es igual al n¨²mero que os encontr¨¦is en la fila siguiente, pero en la diagonal contraria. En la siguiente imagen ten¨¦is algunos ejemplos para que lo entend¨¢is mejor:

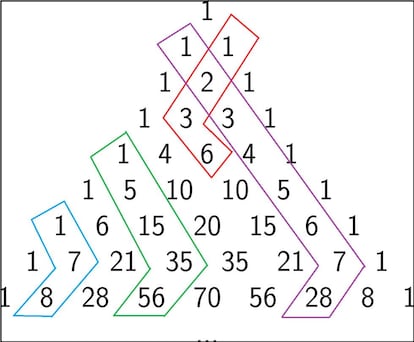
Vamos ahora con alguna caracter¨ªstica menos evidente, m¨¢s rebuscada: podemos encontrar la sucesi¨®n de Fibonacci en el tri¨¢ngulo de Pascal. La sucesi¨®n de Fibonacci, para quien no la conozca, comienza con F₁=1 y F₂=1, y el resto de t¨¦rminos se forman sumando los dos anteriores: F_n=F_n-1+F_n-2. Concretamente, ser¨ªa ¨¦sta: 1, 1, 2, 3, 5, 8, 13, 21, 34, etc. ?C¨®mo encontrarla? Echa un ojo a la siguiente imagen:

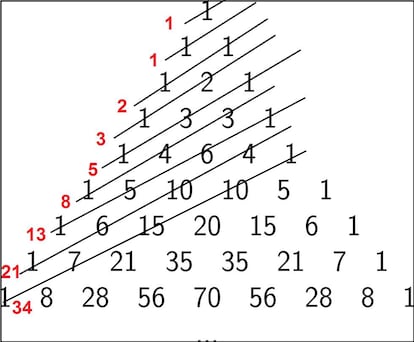
La sucesi¨®n de Fibonacci, muy estudiada y muy comentada en internet (y de la que igual hablamos con mayor profundidad en pr¨®ximos art¨ªculos), aparece en multitud de situaciones en la que no se la esperaba, como ocurre en el tri¨¢ngulo de Pascal. Hay m¨¢s sucesiones num¨¦ricas con esa caracter¨ªstica, como la de los n¨²meros de Catalan, llamada as¨ª por el matem¨¢tico belga Eug¨¨ne Catalan. Dicha sucesi¨®n comienza as¨ª: 1, 1, 2, 5, 14, 42, 132¡­ La forma en la que se construye esta sucesi¨®n es un poco m¨¢s compleja, pero si alguien est¨¢ interesado en verla la tiene aqu¨ª.

?D¨®nde est¨¢n los n¨²meros de Catalan en el tri¨¢ngulo de Pascal? Muy sencillo: tomad la columna central y restadle a cada elemento el n¨²mero que aparece a su lado en el tri¨¢ngulo:

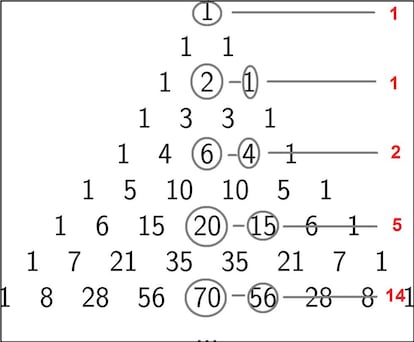
Como pod¨¦is ver, en el tri¨¢ngulo de Pascal aparecen tanto n¨²meros pares como n¨²meros impares. Pues si quitamos los pares obtenemos una bonita disposici¨®n fractal, conocida como tri¨¢ngulo de Sierpinski:

Y ahora un par de sorpresas que nos da esta magn¨ªfica construcci¨®n. Para la primera, vamos a trabajar de la siguiente forma. Hemos visto propiedades en las que hay que localizar n¨²meros, otras en las que hay que sumar los elementos colocados en ciertas posiciones¡­pero no hemos visto qu¨¦ ocurre al multiplicar elementos. Pues bien, multipliquemos los elementos de cada fila. Obtenemos as¨ª la siguiente lista de n¨²meros:

{1, 1, 2, 9, 96, 2500, 162000,¡­}

Vamos ahora a dividir cada n¨²mero de esa lista entre el anterior, obteniendo esta nueva lista:

{1, 2, 4¡¯5, 10¡¯666¡­, 26¡¯0417, 64,8,¡­}

Y ahora volvemos a hacer lo mismo, dividimos cada n¨²mero de esta nueva lista entre el anterior. Nos queda lo siguiente:

{2, 2¡¯25, 2¡¯370370¡­, 2¡¯44140625, 2¡¯48832,¡­}

Y paramos de dividir. Si analizamos lo que ocurre conforme aumenta el valor de n, tenemos que los valores de esta lista se acercan cada vez m¨¢s al n¨²mero e. Es decir, realizando las operaciones descritas podemos encontrar el n¨²mero e en el tri¨¢ngulo de Pascal. Pod¨¦is ver una demostraci¨®n de este resultado aqu¨ª.

Seguro que, conforme hab¨¦is ido leyendo este art¨ªculo, algunos de vosotros os hab¨¦is preguntado si hay alguna forma de encontrar el n¨²mero ¦Ð en este tri¨¢ngulo. Pues s¨ª, se puede encontrar el n¨²mero ¦Ð en el tri¨¢ngulo de Pascal. Y no s¨®lo de una manera, sino de (que yo sepa) al menos de dos formas. Dada la complejidad de las mismas, tanto por los conocimientos previos necesarios como por su explicaci¨®n, os dejo un enlace en el que pod¨¦is ver la explicaci¨®n de este maravilloso hecho.

Y para finalizar con la descripci¨®n de curiosidades de esta maravilla de las matem¨¢ticas, no pod¨ªan faltar las conjeturas. Todo objeto matem¨¢tico que se precie debe tener alguna conjetura asociada a ¨¦l, y el tri¨¢ngulo de Pascal no pod¨ªa ser menos. Es claro que, excepto el 1, todo n¨²mero entero positivo aparece en el tri¨¢ngulo de Pascal un n¨²mero finito de veces (?por qu¨¦?). En relaci¨®n con esto, se conjetura (todav¨ªa no est¨¢ ni demostrado ni refutado) que existe un n¨²mero M tal que ning¨²n entero positivo aparece m¨¢s de M veces en nuestro tri¨¢ngulo. Esto es, que el n¨²mero de apariciones de un entero positivo en el tri¨¢ngulo de Pascal est¨¢ acotado superiormente, y adem¨¢s esta cota no depende del n¨²mero. Esta conjetura se denomina conjetura de Singmaster, y la verdad es que, aunque se cree que es cierta, no se tiene mucha informaci¨®n sobre cu¨¢l podr¨ªa ser la cota. Se sabe que hay un n¨²mero, el 3003, que aparece ocho veces en el tri¨¢ngulo, y no se conoce ninguno m¨¢s que aparezca tantas veces. Se piensa que la cota puede ser, como mucho, 10 o 12. Pero lo dicho, por ahora no tenemos m¨¢s informaci¨®n.

Este tri¨¢ngulo tiene muchas otras propiedades que son dignas de destacar, y seguro que muchos de vosotros conoc¨¦is alguna que no hayamos comentado por aqu¨ª. Ser¨ªa interesante que, en ese caso, nos las mostrarais en los comentarios. Y para los que no sep¨¢is ninguna m¨¢s (bueno, tambi¨¦n para los que s¨ª conoc¨¦is alguna) os dejo un ejercicio para que pens¨¦is. En el tri¨¢ngulo de Pascal tambi¨¦n tiene cierta relaci¨®n con los n¨²meros de Mersenne y, por consiguiente, con n¨²meros perfectos. A ver qui¨¦n la encuentra y nos lo explica en los comentarios.