El Tangram, Bolyai-Gerwien y la cuadratura del c¨ªrculo

Quien m¨¢s quien menos ha visto alguna vez un Tangram, ese juego de origen chino consistente en 7 piezas, que inicialmente est¨¢n dispuestas en forma de cuadrado, con las que se pueden formar una gran variedad de figuras planas. En la siguiente imagen pod¨¦is ver la disposici¨®n inicial de las piezas del Tangram y algunos ejemplos de figuras planas creadas con dichas piezas:

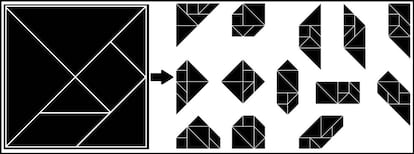
Si trasladamos esto a papel, tendr¨ªamos que podemos cortar un cuadrado en un cierto n¨²mero de piezas (siete concretamente en el caso del Tangram) que pueden reordenarse para formar otras figuras (pol¨ªgonos en el caso de la imagen anterior). Un ejemplo muy conocido de esto es la llamada disecci¨®n de Dudeney, que transforma un cuadrado en un tri¨¢ngulo de la misma ¨¢rea. Esta disecci¨®n tiene, adem¨¢s, la particularidad de que se pasa de una figura a otra girando las piezas cortadas mientras ¨¦stas permanecen unidas en parejas por un v¨¦rtice. Pod¨¦is ver varias secuencias en la siguiente imagen:

En prof.pantaloni ten¨¦is la disecci¨®n completa animada en un gif.

A partir de esto, nos podr¨ªamos preguntar si, dado un pol¨ªgono cualquiera de la misma ¨¢rea que un cuadrado, existir¨ªa alguna manera de cortar el cuadrado en piezas de forma que se puedan recolocar para formar dicha figura. M¨¢s general: si tenemos dos pol¨ªgonos cualesquiera de la misma ¨¢rea, ?podemos cortar uno en trocitos que puedan reordenarse para formar el otro? Pues la respuesta es que s¨ª se puede, y eso nos lo asegura el llamado teorema de Bolyai-Gerwien, que se puede enunciar informalmente como sigue:

Teorema de Bolyai-Gerwien: Dados dos pol¨ªgonos de la misma ¨¢rea, se puede cortar uno de ellos en un n¨²mero finito de piezas poligonales que, mediante traslaciones y giros, pueden colocarse formando el otro pol¨ªgono.

Este resultado fue conjeturado por Farkas Bolyai en 1790 y demostrado por primera vez por el matem¨¢tico William Wallace (nada que ver con el protagonista de Braveheart) en 1807 (por ello, a veces este resultado se llama teorema de Wallace-Bolyai-Gerwien). En 1833, P. Gerwien (no he conseguido encontrar informaci¨®n fiable sobre qu¨¦ significa exactamente esa P) demostr¨® este teorema sin conocer la demostraci¨®n anterior de Wallace, y en 1835 el propio Bolyai encontr¨® una demostraci¨®n tambi¨¦n sin tener conocimiento de las pruebas anteriores de Wallace y Gerwien.

Informalmente, las l¨ªneas generales de la demostraci¨®n son las siguientes:

1.- Todo pol¨ªgono puede cortarse en piezas triangulares.

2.- Esas piezas triangulares pueden reordenarse formando rect¨¢ngulos.

3.- Colocando conveniente esos rect¨¢ngulos, se puede formar un ¨²nico rect¨¢ngulo.

4.- Un rect¨¢ngulo puede recortarse en piezas con las que se puede formar un cuadrado.

5.- Como este proceso puede realizarse con los dos pol¨ªgonos, lo que hacemos es pasar de uno de ellos a un cuadrado y despu¨¦s pasar de ese cuadrado al otro pol¨ªgono (invirtiendo el proceso de cuadrar este pol¨ªgono).

Y as¨ª conseguimos llevar un pol¨ªgono a otro pol¨ªgono mediante disecciones. Aqu¨ª ten¨¦is algunos ejemplos de pasos de un pol¨ªgono a otro:

Pod¨¦is ver muchos m¨¢s en Geometric Dissections, de Gavin Theobald (web de donde he sacado las disecciones anteriores).

Sabiendo esto, surge de manera natural preguntarse sobre qu¨¦ ocurre en tres dimensiones. Y esta cuesti¨®n es tan interesante que el propio David Hilbert la incluy¨® dentro de su famosa lista de 23 problemas que propuso en el Congreso Internacional de Matem¨¢ticos celebrado en Par¨ªs en el a?o 1900. El tercero de los problemas de dicha lista es el que hace alusi¨®n a este tema:

Dados dos poliedros del mismo volumen, ?siempre se puede cortar uno de ellos en un n¨²mero finito de piezas poli¨¦dricas que puedan reordenarse de manera que formen el segundo poliedro?

?Qu¨¦ cre¨¦is? Os dejo unos segundos para pensarlo¡­

¡­?Ya? Pues la respuesta es no, no siempre se puede hacer lo que pregunta el tercer problema de Hilbert, y esta imposibilidad general fue demostrada por Max Dehn en el mismo a?o 1900.

Y, volviendo a las dos dimensiones, tambi¨¦n surgi¨® una interesante y curiosa pregunta que, en esta ocasi¨®n, se hizo Alfred Tarski. Este matem¨¢tico polaco se pregunt¨® si se podr¨ªa pasar de un cuadrado a un c¨ªrculo de la misma ¨¢rea de una forma parecida a lo que se puede hacer entre pol¨ªgonos (nada que ver con la cuadratura del c¨ªrculo cl¨¢sica, ya que aqu¨ª no tenemos las restricciones de las construcciones griegas con regla y comp¨¢s). ?Cu¨¢l cre¨¦is que es la respuesta en este caso? De nuevo, unos segundos para que pens¨¦is y respond¨¢is¡­

¡­

¡­??Tiempo!! La respuesta en este caso es que s¨ª, s¨ª se puede, aunque la cosa tiene ¡°truco¡±. Tarski conjetur¨® que s¨ª se pod¨ªa pasar de un cuadrado a un c¨ªrculo, y el matem¨¢tico h¨²ngaro Mikos Laczkovich lo demostr¨® en 1990 en su trabajo Equidecomposability and discrepancy; a solution of Tarski¡¯s circle-squaring problem. La demostraci¨®n de Laczkovich nos dice que necesitar¨ªamos, como mucho, 10⁵⁰ piezas (casi nada), y que las mismas son no medibles (sin entrar en detalles, raras raras) y, por tanto, ni mucho menos ¡°cortables¡±.

El hecho de que no se puede pasar de un c¨ªrculo a un cuadrado con piezas ¡°cortables con tijeras¡± ya lo hab¨ªan demostrado Lester Dubins, Morris Hirsch y Jack Karush en 1963, pero hasta hace poco segu¨ªa sin saberse si se pod¨ªa hacer, al menos, con piezas medibles. El propio Laczkovich hablaba en su trabajo sobre este asunto, y lo dejaba planteado como, posiblemente, la pregunta m¨¢s importante que quedaba por resolver en relaci¨®n con este tema.

Bien, pues ya se ha resuelto. En el trabajo Measurable circle squaring (que ser¨¢ publicado pr¨®ximamente en la prestigiosa revista Annals of Mathematics), Lukasz Grabowski, Andr¨¢s M¨¢th¨¦ y Oleg Pikhurko han demostrado que s¨ª se puede pasar de un c¨ªrculo a un cuadrado con piezas medibles. Es decir, que existe una cierta cantidad finita de piezas medibles que al colocarlas de cierta manera nos dan un cuadrado y convenientemente trasladadas nos dan un c¨ªrculo.

Usando s¨®lo traslaciones, este n¨²mero de piezas (seg¨²n los autores) est¨¢ entre 4 y 10⁵⁰ (la cota de Laczkovich), por lo que queda todav¨ªa un gran margen para mejorar el resultado.