Una igualdad rebosante de belleza

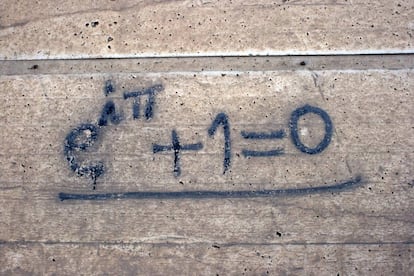
Al igual que en otras disciplinas, como la literatura, el arte o la m¨²sica, dentro de las matem¨¢ticas tambi¨¦n podemos encontrar belleza, mucha belleza. La geometr¨ªa es, posiblemente, una de las ramas donde se pueden encontrar resultados m¨¢s bellos (como, por ejemplo, el de la circunferencia de Feuerbach), pero tambi¨¦n podemos encontrar bellezas matem¨¢ticas jugando con n¨²meros (los cuadrados m¨¢gicos habituales y los menos habituales son buenos ejemplos de ello).

Pero estoy convencido de que la igualdad que os traigo hoy es, para muchos, el culmen de la belleza matem¨¢tica. Me refiero, c¨®mo no, a la identidad de Euler:

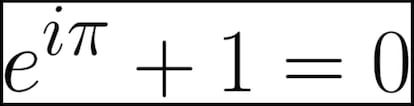
Ni ecuaci¨®n (no hay en ella ninguna inc¨®gnita) ni f¨®rmula (no hay ninguna relaci¨®n entre magnitudes): igualdad o identidad de Euler. La identidad de Euler es una igualdad que relaciona de una manera preciosa cinco de los n¨²meros m¨¢s importantes y representativos de las matem¨¢ticas: 0, 1, e, i y ¦Ð. Y hoy vamos a explicar c¨®mo se lleg¨® a esa maravillosa relaci¨®n.

La identidad de Euler es un caso particular de la conocida como f¨®rmula de Euler (no confundir con la f¨®rmula de Euler para poliedros), aunque Roger Cotes ya public¨® algo relacionado con ella antes que Euler (aunque no escrita de la forma habitual). La f¨®rmula en cuesti¨®n aparece en Introductio in analysin infinitorum, posiblemente la obra m¨¢s conocida e importante del gran Leonhard Euler. En la p¨¢gina 104 del Volumen I de la misma podemos ver c¨®mo un desarrollo anterior culmina en la siguiente expresi¨®n:

Tomando v como un ¨¢ngulo, y sabiendo que en la actualidad a ¡Ì-1 se representa con la letra i, tenemos la que ahora conocemos como f¨®rmula de Euler:

Aunque en este blog nos dedicamos a la divulgaci¨®n matem¨¢tica a nivel general, no queremos renunciar a los desarrollos matem¨¢ticos. Por ello, a continuaci¨®n presentamos una demostraci¨®n de dicha f¨®rmula.

Partimos de la expresi¨®n de e^x como serie de potencias:

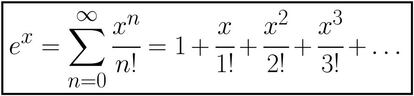
En ella, sustituimos x por iz. Usando que i¹=i, i²=-1, i³=-I y que i⁴=1 (y que el ciclo se repite de ah¨ª en adelante), y separando despu¨¦s los t¨¦rminos de exponente par por un lado y los de exponente impar por otro tenemos lo siguiente:

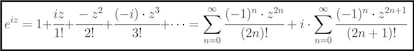
Y da la maravillosa casualidad de que los desarrollos en serie de cos(z) y sen(z) son exactamente esas dos ¨²ltimas series (y en ese orden). Por tanto, ya tenemos la esperada y buscada f¨®rmula de Euler:

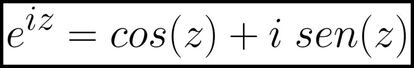
La identidad de Euler, protagonista de este art¨ªculo, sale de la f¨®rmula de Euler al sustituir z por ¦Ð, sabiendo que cos(¦Ð)=-1 y sen(¦Ð)=0 y sumando 1 a ambos lados de la ecuaci¨®n:

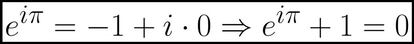
La tremenda belleza que rodea a esta identidad hace que aparezca de manera recurrente en muchos lugares. Es magn¨ªfica para aparecer en obras de arte, y los grafitis dan una buena prueba de ello. Hay muchos que tienen a la identidad de Euler como protagonista, y concretamente en Granada podemos encontrar unos cuantos. En la imagen ten¨¦is un par de ejemplos. A la izquierda ten¨¦is una que se puede ver en la calle Gonzalo Gallas, saliendo por la puerta trasera de la Facultad de Ciencias (much¨ªsimas gracias a Antonio Bueno por acercarte a hacer la foto y por envi¨¢rmela). Y a la derecha ten¨¦is otra en la pared de una casa en el campo que encuentra en alguna de las salidas que hay en la autov¨ªa Jaen-Granada:

Tengo que agradecer a Modesto, el autor de la foto, que se haya preocupado por buscarla y mand¨¢rmela. Espero que pararas para hacerla, ya que admirar tanta belleza matem¨¢tica en una sola expresi¨®n podr¨ªa provocar un accidente.

Por cierto, en Pintando Granada pod¨¦is ver otro grafiti de la identidad de Euler que puede contemplarse en esta maravillosa ciudad.

Tambi¨¦n podemos encontrarla en esa maravillosa serie de humor que lleva retratando a la sociedad americana (bueno, y a la mundial) desde hace muchos muchos a?os: Los Simpson. El frikismo cient¨ªfico es una caracter¨ªstica com¨²n a gran parte de sus guionistas (Manuel Ansede nos habl¨® de ello, centrado en las matem¨¢ticas, en Los diez mejores momentos matem¨¢ticos de ¡®Los Simpson¡¯), y ello ha propiciado que esta identidad aparezca en varios cap¨ªtulos. Aqu¨ª ten¨¦is algunas im¨¢genes de los mismos:

Y, c¨®mo no, es tambi¨¦n perfecta para modificaciones corporales. Es habitual verla en tatuajes, como ¨¦ste que Eva me envi¨® hace tiempo:

o en ¨¦ste del gran Eugenio, autor del blog Ciencia en el XXI:

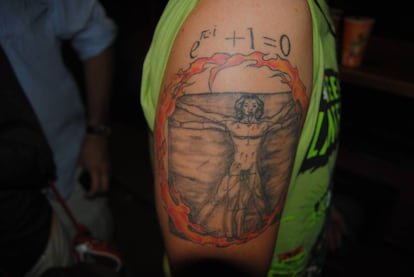
Y tambi¨¦n es protagonista es escarificaciones, como puede verse en esta impactante imagen:

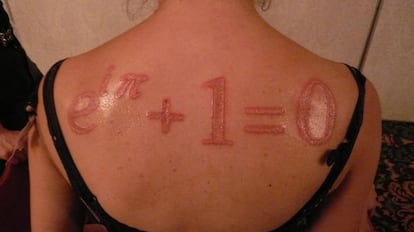
Seguro que vosotros conoc¨¦is otros lugares en los que aparece. Os agradeceremos muchos que compart¨¢is vuestras experiencias y vuestras im¨¢genes en los comentarios.