El n¨²mero m¨¢s grande jam¨¢s citado

Piensa un n¨²mero grande, muy grande, el n¨²mero (con alg¨²n nombre o significado) m¨¢s grande del que hayas visto, le¨ªdo u o¨ªdo algo. Quiz¨¢s te haya venido a la cabeza un bill¨®n, que es un 1 seguido de 12 ceros. S¨ª, es grande, pero seguro que tambi¨¦n has escuchado a alguien nombrar al trill¨®n, que es un mill¨®n de billones (formado entonces por un 1 seguido de 18 ceros) y que, por tanto, es mayor que un bill¨®n.

Pero seguro que muchos habr¨¦is pensado en otros m¨¢s grandes, como el googol (o g¨²gol). Este n¨²mero est¨¢ formado por un 1 seguido de 100 ceros y, seg¨²n parece, inspira el nombre del buscador m¨¢s famoso de internet (ya hemos comentado por aqu¨ª que los chicos de Google son bastante frikis).

S¨ª, este n¨²mero es muy grande, mucho mayor que el n¨²mero de ¨¢tomos del Universo conocido, 10⁸⁰. Pero en?realidad solamente tiene 101 cifras, por lo que es sencillo de expresar con la notaci¨®n de exponentes habitual: 10¹⁰⁰.

Antes de seguir, es interesante aclarar que en este art¨ªculo hablamos de n¨²meros naturales conocidos. Est¨¢ claro que los n¨²meros naturales son infinitos, por lo que, en teor¨ªa, podr¨ªamos escribir un n¨²mero todo lo grande que quisi¨¦ramos, y despu¨¦s de escrito podr¨ªamos escribir otro mayor sum¨¢ndole 1, multiplic¨¢ndolo por 7 o elev¨¢ndolo al cuadrado. La intenci¨®n de este art¨ªculo es hablar de n¨²meros de los cuales conozcamos su descripci¨®n y que tengan cierta relevancia dentro de las matem¨¢ticas.

Aclarado esto, volvamos a los n¨²meros. Los conocemos mucho m¨¢s grandes que el googol, y en este blog hemos hablado de ellos: algunos primos de Mersenne. Concretamente, el m¨¢s grande que conocemos tiene m¨¢s de 22 millones de d¨ªgitos. Como dec¨ªamos en ese art¨ªculo, un n¨²mero descomunal¡­

¡­pero todav¨ªa se puede expresar de manera c¨®moda con la notaci¨®n que solemos utilizar para los exponentes:

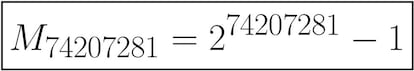
Con el protagonista del art¨ªculo de hoy no vamos a tener tanta suerte, es tan grande que la notaci¨®n exponencial que conocemos se nos queda corta, por lo que necesitaremos una forma nueva de escribir las operaciones habituales. Hablamos del n¨²mero de Graham.

Antes de hablar de ¨¦l, vamos a hacer alg¨²n comentario sobre el contexto en el que apareci¨®, aunque no daremos muchas explicaciones sobre el mismo. Nos situamos en la rama conocida como teor¨ªa de Ramsey y nos planteamos el siguiente problema:

Consideramos un hipercubo de dimensi¨®n n y conectamos cada pareja de v¨¦rtices, obteniendo un grafo completo de 2ⁿ v¨¦rtices. Despu¨¦s, coloreamos cada arista de negro o rojo. ?Cu¨¢l es el menor valor de n para el que toda manera de colorear las aristas necesariamente nos proporciona un subgrafo completo de un solo color con cuatro v¨¦rtices que forman un plano?

El problema es complicado de entender, y m¨¢s a¨²n de resolver, pero en este art¨ªculo no nos interesa profundizar en ¨¦l. La cuesti¨®n es que Ronald Graham y Bruce Rothschild demostraron que el problema ten¨ªa soluci¨®n, y dieron una cota de la misma. M¨¢s adelante, en un art¨ªculo no publicado, Graham rectific¨® esa cota al alza, que a partir de ah¨ª (gracias tambi¨¦n a que Martin Gardner habl¨® sobre ella en su famosa columna en Scientific American) se comenz¨® a llamar n¨²mero de Graham.

Bien, as¨ª que este n¨²mero es una cota superior de un cierto valor que aparece en una demostraci¨®n matem¨¢tica, por lo que en cierto modo es importante. Pero, ?cu¨¢l es exactamente ese n¨²mero? Vamos a verlo.

Como coment¨¢bamos unos p¨¢rrafos m¨¢s arriba, la notaci¨®n que usamos habitualmente para describir n¨²mero naturales se nos queda corta, por lo que necesitamos una nueva forma de escribir n¨²meros. Esta nueva operaci¨®n se denomina notaci¨®n flecha de Knuth, en honor a su inventor, Donald Knuth. Veamos en qu¨¦ consiste.

Todos sabemos que cuando escribimos 4³ lo que hacemos es abreviar la operaci¨®n 4 ¡¤ 4 ¡¤ 4. Es decir, multiplicamos la base, 4, el n¨²mero de veces que dice el exponente, 3. Bien, pues vamos a cambiar la forma de escribir esa operaci¨®n: ahora es 4¡ü3.

Comencemos a generalizar. Si con una flecha multiplicamos la base el n¨²mero de veces que diga el exponente, ?c¨®mo definir¨ªamos la operaci¨®n que quedar¨ªa al poner dos flechas? Pues muy sencillo: dos flechas implican operar ¡°flecha¡± el n¨²mero de la izquierda la cantidad de veces que indique el n¨²mero de la derecha. Es decir, lo siguiente:

4¡ü¡ü3 = 4¡ü(4¡ü4)

Es decir, operamos flecha el n¨²mero 4 (izquierda) tres veces (derecha). ?Y tres flechas? Pues, siguiendo el razonamiento anterior, tres flechas significan operar ¡°dos flechas¡± el n¨²mero de la izquierda la cantidad de veces que diga el de la derecha, que luego a su vez se pueden desglosar cada una de ellas en una sola flecha:

4¡ü¡ü¡ü3 = 4¡ü¡ü(4¡ü¡ü4) = 4¡ü¡ü(4¡ü(4¡ü(4¡ü4))) = ¡­

Y as¨ª podr¨ªamos seguir poniendo flechas y definiendo cada una de las operaciones en funci¨®n de la anterior: cuatro flechas se desglosar¨ªan en varias tres flechas, cinco flechas en varias cuatro flechas, y as¨ª sucesivamente.

Estas ¡°operaciones flecha¡± hacen que los n¨²meros que vamos obteniendo con cada una de ellas crezcan de una manera bestial conforme a?adimos flechas. Para intentar que os hag¨¢is una peque?a idea, aqu¨ª os dejo los valores de algunas de ellas. Tened en cuenta que he usado n¨²meros muy peque?os, imaginad los resultados que podr¨ªan salir con n¨²meros m¨¢s grandes:

Bien, vayamos ya (por fin) a nuestro n¨²mero de Graham, que llamaremos G. Graham lo describi¨® de la siguiente forma:

¡¤ Construimos 3¡ü¡ü¡ü¡ü3, y lo llamamos g₁. Teniendo en cuenta que 3¡ü¡ü¡ü3 es una torre de exponentes que contiene 7625597484987 treses, no os digo nada sobre cu¨¢ntos treses tiene este n¨²mero g₁.

¡¤ Ahora, llamamos g₂ al n¨²mero 3¡ü¡ü¡­(g₁ flechas)¡­ ¡ü¡ü3. Como g₁ es enorme, colocar g₁ flechas es una barbaridad. Para calcularlo, habr¨ªa que quitar una flecha y colocar tres treses con una flecha menos; despu¨¦s quitar otra flecha de cada una de las que han quedado y hacer las operaciones necesarias con una flecha menos, y as¨ª sucesivamente hasta que lleguemos a una flecha. Vamos, un n¨²mero DESCOMUNAL.

¡¤ En el siguiente paso, llamamos g₃ al n¨²mero 3¡ü¡ü¡­(g₂ flechas)¡­ ¡ü¡ü3. Si g₂ era ya algo realmente grande, meter g₂ flechas da un n¨²mero que no podemos ni imaginar.

¡¤ Continuamos as¨ª hasta g₆₄. Es decir, g₆₄=3¡ü¡ü¡­(g₆₃ flechas)¡­ ¡ü¡ü3. Pues ¨¦ste es G, el n¨²mero de Graham. Si los anteriores eran grandes, enormes, descomunales, inimaginables¡­imaginad c¨®mo puede ser ¨¦ste¡­

¡­o mejor no, mejor no intent¨¦is imaginarlo, es absolutamente imposible hacerse una m¨ªnima idea de la aut¨¦nticamente bestial magnitud de este n¨²mero de Graham.

?Cu¨¢l fue el razonamiento que llev¨® a Ronald Graham a obtener semejante monstruosidad de n¨²mero? Pues la verdad es que no lo s¨¦, y sinceramente no me importa. Saber de la existencia de este n¨²mero me llev¨® a conocer una nueva curiosidad matem¨¢tica y tambi¨¦n a descubrir una nueva manera de representar n¨²meros muy muy grandes. Para m¨ª, eso es suficiente.

Actualmente, la cota para este problema es m¨¢s baja, aunque sigue requiriendo de la notaci¨®n flecha de Knuth para describirla. Por otra parte, en algunas otras demostraciones han aparecido valores de ciertas funciones ¡°extra?as¡± que, seg¨²n parece, son n¨²meros mayores que este n¨²mero de Graham, pero es relativamente reciente. En la actualidad, podemos decir que el n¨²mero de Graham sigue ocupando el primer puesto en lo que respecta a magnitud de un n¨²mero aparecido en una demostraci¨®n matem¨¢tica. Y, como hemos podido ver a lo largo de este art¨ªculo, ese primer puesto es total y absolutamente merecido.