?Por qu¨¦ las alcantarillas son redondas?

?Te has fijado en las alcantarillas que suele haber en las calles? S¨ª, las que hay en la calzada. ?Te hab¨ªas dado cuenta de que son todas redondas? Posiblemente s¨ª, pero tambi¨¦n es posible que no hayas pensado en el porqu¨¦. En este art¨ªculo vamos a ver una raz¨®n relacionada con las matem¨¢ticas que explica que estas alcantarillas tenga siempre esa forma, y adem¨¢s intentaremos ampliar un poco nuestros conocimientos sobre figuras geom¨¦tricas presentando algunas que, a pesar de no son c¨ªrculos, se comportan como ellos en cierto sentido.

Como dec¨ªamos, hablamos de las t¨ªpicas alcantarillas que podemos encontrarnos en la calzada:

La raz¨®n matem¨¢tica que puede explicar esta forma es muy sencilla: que no se nos caiga la tapa por el agujero. Y s¨ª, ¨¦sta es una raz¨®n matem¨¢tica. Veamos por qu¨¦.

Si llamamos anchura de una figura plana a la distancia que hay entre dos puntos opuesto del borde de la misma, se cumple que el c¨ªrculo es de anchura constante, ya que la distancia que podemos encontrar entre dos puntos opuestos de su borde (que es una circunferencia) es siempre la misma, el di¨¢metro. Esto implica, en nuestro caso, que si colocamos la tapa en el agujero de la alcantarilla, es imposible que dicha tapa entre por el agujero.

?Qu¨¦ ocurrir¨ªa si la tapa fuera, por ejemplo, cuadrada o rectangular? Pues que en estos casos la anchura no es constante, ya que, por ejemplo, la distancia entre dos v¨¦rtices opuestos (la diagonal de cualquiera de ellos) es mayor que cualquiera de los lados (Pit¨¢goras dixit). Eso, en el caso de las alcantarillas, significa que la tapa cabe por el agujero si la metemos en diagonal, por lo que corremos el riesgo de que se nos caiga por ¨¦l, con el gran problema que eso podr¨ªa conllevar dada la profundidad que suelen tener esas alcantarillas. Pod¨¦is ver las dos situaciones, tapas circulares y tapas rectangulares/cuadradas, en este enlace de Live Science.

Ahora, seguro que muchos est¨¢is pensando que hab¨¦is visto muchas tapas cuadradas y rectangulares en las calles de vuestra ciudad, ?verdad? Pues s¨ª, las hay:

?Aqu¨ª no hay peligro? Pues no, ya que lo habitual es que estas tapas est¨¦n colocadas para tapar agujeros con muy poca profundidad, con lo que si no colocamos bien la tapa, o se nos resbala y se nos cae, podremos cogerla f¨¢cilmente.

Bien, explicada la raz¨®n por la que conviene tapar agujeros muy profundos con tapas circulares (en vez de rectangulares o cuadradas), tendr¨ªa sentido preguntarse si ¨¦sa es la ¨²nica opci¨®n. Lo normal es que digamos que s¨ª, que visto lo visto la ¨²nica figura que tiene las propiedades que deseamos es el c¨ªrculo. Pues la verdad es que hay m¨¢s, de hecho hay infinitas m¨¢s.

La m¨¢s conocida es el tri¨¢ngulo de Reuleaux, creado por el ingeniero alem¨¢n Franz Reuleaux en el siglo XIX, al parecer para dise?ar un bot¨®n que no tuviera forma circular pero que s¨ª estuviera en posesi¨®n de la propiedad de anchura constante, aunque esta figura ya apareci¨® en algunos escritos de Leonardo da Vinci y fue objeto de estudio por parte de Leonhard Euler (?hay alg¨²n sitio en el que no aparezca el gran Euler?).

Este tri¨¢ngulo de Reuleaux es f¨¢cil de construir. Partimos de un tri¨¢ngulo equil¨¢tero y despu¨¦s trazamos tres circunferencias cuyo centro sea cada uno de los v¨¦rtices y cuyo radio sea el lado del tri¨¢ngulo. La figura que queda en la parte central es la conocida como tri¨¢ngulo de Reuleaux. Pod¨¦is ver la construcci¨®n y la figura en la siguiente imagen:

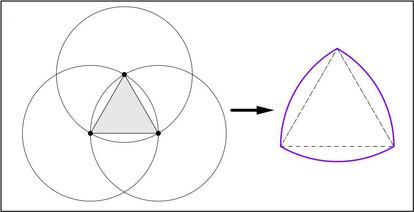
Y como m¨¢s de uno habr¨¢ pensado ya, el tri¨¢ngulo de Reuleaux se puede generalizar a todo pol¨ªgono regular con un n¨²mero impar de lados, obteniendo as¨ª los llamados pol¨ªgonos de Reuleaux. Como existen infinitos pol¨ªgonos regulares, tambi¨¦n existen infinitos pol¨ªgonos de Reuleaux (por esto dec¨ªamos antes que hay infinitas figuras con anchura constante). En la imagen siguiente pod¨¦is ver los pol¨ªgonos de Reuleaux asociados a un pent¨¢gono regular y a un hept¨¢gono regular junto al tri¨¢ngulo de Reuleaux:

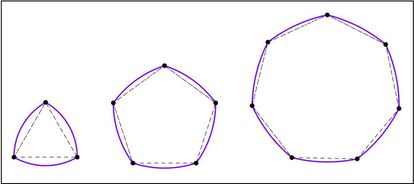
Estas curiosas figuras, por su propiedad de anchura constante, pueden usarse en multitud de situaciones en las que habitualmente vemos c¨ªrculos. Por ejemplo, pueden utilizarse como moneda, ya que es apta para su uso en m¨¢quinas expendedoras o m¨¢quinas de juego (estas m¨¢quinas se gu¨ªan por la anchura de las monedas para clasificarlas). ?Qu¨¦ os parecer¨ªa raro ver una moneda as¨ª? Pues las hay. En Reino Unido las usan para las monedas de 20 y 50 peniques.

Tambi¨¦n pueden usarse como brocas, ya que tienen una propiedad muy peculiar: las brocas en forma de pol¨ªgono de Reuleaux hacen agujeros ¡°casi¡± cuadrados. Pod¨¦is verlo en este enlace. Y tambi¨¦n se ha usado en arquitectura y en dise?o de l¨¢pices. Y seguro que en muchas cosas m¨¢s. Os animo a que compart¨¢is m¨¢s objetos y construcciones que tenga forma de tri¨¢ngulo de Reuleaux, seguro que encontr¨¢is algunas que no se han nombrado aqu¨ª.

Volviendo al comienzo de este art¨ªculo, estoy seguro de que ya tenemos claro que el tri¨¢ngulo de Reuleaux (y, en general, cualquier pol¨ªgono de Reuleaux) tambi¨¦n se puede usar para dise?ar el agujero y la tapa de una alcantarilla. Pero bueno, no creo que haya nadie tan friki como para dise?ar una alcantarilla con esta forma¡­

¡­?nadie? ?Seguro? Amigos m¨ªos, si hab¨ªais pensado eso os equivoc¨¢is de pleno: hay alcantarillas con forma de tri¨¢ngulo de Reuleaux. Aqu¨ª ten¨¦is una que se encuentra en San Francisco:

Preciosa, ?verdad? A ver si alguien encuentra alguna m¨¢s y nos env¨ªa una foto.