Un problema que vale un mill¨®n de d¨®lares

Normalmente, al demostrar un resultado matem¨¢tico uno se contenta con la satisfacci¨®n que produce la resoluci¨®n del problema en cuesti¨®n, pero, siendo sinceros, no est¨¢ de m¨¢s que en ocasiones ese trabajo tenga alg¨²n tipo de premio adicional. Hay muchos problemas, actualmente sin resolver, que tienen asignada una dotaci¨®n econ¨®mica. Vamos, que si los resuelves te llevas pasta, adem¨¢s del orgullo personal y de la fama que adquirir¨ªas en el mundillo.

Los hay con un premio peque?o, testimonial, y tambi¨¦n los podemos encontrar con premios bastante apetecibles. Los m¨¢s conocidos son los problemas del milenio, que son los siguientes:

P versus NP

La conjetura de Hodge

La hip¨®tesis de Riemann

La conjetura de Poincar¨¦

La conjetura de Birch y Swinnerton-Dyer

Las ecuaciones de Navier-Stokes

Existencia de Yang-Mills y el salto de masa

Fueron propuestos en el a?o 2000, A?o Mundial de las Matem¨¢ticas, por el Instituto Clay y cada uno de ellos est¨¢ dotado con un premio de un mill¨®n de d¨®lares. El ¨²nico que se ha resuelto hasta el d¨ªa de hoy es la conjetura de Poincar¨¦, que fue demostrada afirmativamente por Grisha Perelman en 2003. Curiosamente, Perelman no acept¨® el premio en met¨¢lico, ni tampoco la Medalla Fields, uno de los galardones m¨¢s importantes de los que se otorgan a matem¨¢ticos, que se le concedi¨® en 2006.

Pero no vamos a hablar hoy de estos problemas del milenio, sino de otro problema menos conocido por el p¨²blico general cuyo premio es tan jugoso como los anteriores: la conjetura de Beal.

Vamos a introducir esta conjetura poco a poco. Seguro que muchos de vosotros hab¨¦is o¨ªdo hablar del llamado ¨²ltimo teorema de Fermat (UTF), propuesto por Fermat en el siglo XVII en el margen de un libro y demostrado por Andrew Wiles unos 300 a?os despu¨¦s, en 1995.Este teorema dice lo siguiente:

La ecuaci¨®n xⁿ+yⁿ=zⁿ no tiene soluciones para x, y,z enteros positivos y n entero positivo mayor que 2.

Para n=2 hay infinitas soluciones, las infinitas ternas de n¨²meros enteros positivos que cumplen el teorema de Pit¨¢goras, las llamadas ternas pitag¨®ricas.

Andrew Beal, un banquero estadounidense de 64 a?os al que le apasionan las matem¨¢ticas, estaba enamorado del trabajo de Fermat, y concretamente de este problema. ?sta debi¨® ser la raz¨®n por la que comenz¨® a pensar en problemas parecidos al UTF en los que se relajara alguna de las condiciones.

Por ejemplo, ?qu¨¦ ocurre si permitimos que los exponentes sean distintos (todos mayores que 1)? Pues que encontramos soluciones (obviamos aqu¨ª las ternas pitag¨®ricas, evidentemente). Aqu¨ª ten¨¦is algunas de ellas:

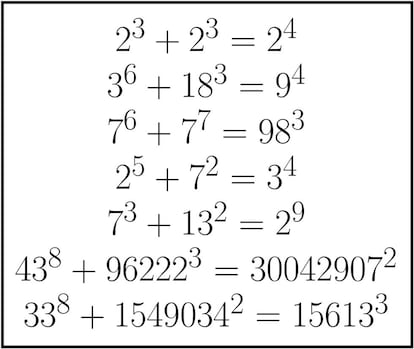
Como pod¨¦is ver, hay soluciones en las que las bases de las potencias tienen alg¨²n factor primo en com¨²n (las tres primeras, que tienen como factor primo com¨²n al 2, al 3 y al 7 respectivamente), y otras en las que no. Descartemos las que tienen bases con factores primos comunes y qued¨¦monos con las otras (en los ejemplos anteriores, las cuatro ¨²ltimas).

De ¨¦stas se conocen unas cuantas soluciones (al parecer, no se conocen demasiadas), y lo curioso de todas estas soluciones (de las conocidas) es que en todas ellas alguno de los exponentes es 2.

Bien, pues con todo esto ya podemos enunciar la conocida como conjetura de Beal:

Si la ecuaci¨®n x^a+y^b=z^c, para x, y, z tres enteros positivos y a, b, c enteros positivos mayores que 2, tiene soluci¨®n, entonces x, y, z tienen alg¨²n factor primo com¨²n.

Este problema fue propuesto, como era de esperar, por Andrew Beal en 1997, y apareci¨® publicado por primera vez en Notices of American Mathematical Society a trav¨¦s del art¨ªculo A Generalization of Fermat¡¯s Last Theorem: The Beal Conjecture and Prize Problem. Para animar a los matem¨¢ticos a que pensaran en ¨¦l, Beal ofreci¨® inicialmente una recompensa de 5000$ para quien resolviera el problema, ya fuera afirmativamente (desarrollando una demostraci¨®n del mismo) o negativamente (por ejemplo, encontrando un contraejemplo). Esta recompensa se ir¨ªa ampliando a?o a a?o hasta los 50000$, pero al no encontrarse soluci¨®n al problema pasado ese tiempo se estableci¨® en 100000$. Finalmente el premio por resolver la conjetura de Beal se ampli¨® a 1 mill¨®n de d¨®lares en junio de 2013.

A d¨ªa de hoy, la conjetura sigue siendo eso, una conjetura. Nadie ha podido demostrarla ni refutarla, por lo que la recompensa sigue ah¨ª, esperando a quien consiga dar respuesta a este problema. Para ello, una resoluci¨®n de la conjetura de Beal debe enviarse al comit¨¦ de la conjetura de Beal, cuyos miembros son Charles Fefferman, Ron Graham y R. Daniel Mauldin. Adem¨¢s, dicho trabajo debe ser publicado por alguna revista matem¨¢tica de prestigio y debe ser aceptado por la comunidad matem¨¢tica (en el caso de que fuera un contraejemplo, debe haber sido verificado como correcto).

Si busc¨¢is un poco por internet, encontrar¨¦is bastantes p¨¢ginas en las que alguien asegura haber demostrado la conjetura de Beal. Ninguna de esas demostraciones cumple las normas impuestas para considerarla correcta: ni se ha verificado por parte del comit¨¦, ni hay revista matem¨¢tica que las haya aceptado. Repito: ninguna. A d¨ªa de hoy, la conjetura de Beal sigue siendo un problema abierto, y no precisamente f¨¢cil de resolver. As¨ª que nada de fiarse de esos charlatanes que dicen haberla demostrado. Yo mismo he recibido alguna que otra supuesta demostraci¨®n de este problema (y de otros, ya os contar¨¦ otro d¨ªa) y normalmente son escritos llenos de razonamientos no demostrados o, directamente, err¨®neos.

Os aseguro que si alguien demostrara esta conjetura adquirir¨ªa fama a nivel mundial, aunque s¨®lo sea por el premio a cobrar por ello, y aportar¨ªa al menos enlaces a la revista donde se public¨® y la nota de prensa que la AMS colgar¨ªa en su web para anunciarlo. Y, muy posiblemente, nosotros lo contar¨ªamos por aqu¨ª y por otros medios. Espero vivir lo suficiente como para poder hablar de tama?a haza?a.