Dirigentes y teoremas
?Conoc¨¦is alg¨²n dirigente relacionado con un resultado matem¨¢tico? Hoy os hablamos de dos de ellos

Hasta donde yo s¨¦, no es muy habitual encontrar dirigentes pol¨ªticos que tengan gusto reconocido por las matem¨¢ticas, y mucho menos que hayan realizado alguna aportaci¨®n interesante dentro de este campo. Pero haberlos, haylos, y en los pr¨®ximos p¨¢rrafos vamos a hablar de dos de ellos y de las matem¨¢ticas que se les atribuyen.
El primero es todo un emperador: Napole¨®n Bonaparte. Es conocido el gusto de Napole¨®n por las matem¨¢ticas y su amistad con matem¨¢ticos muy importantes de su ¨¦poca, como Pierre Simon de Laplace, Joseph-Louis Lagrange y Lorenzo Mascheroni (quedaos con este nombre). Lo que puede que no sea tan conocido es que Napole¨®n da nombre a un teorema matem¨¢tico relacionado con la geometr¨ªa del tri¨¢ngulo.
El conocido como teorema de Napole¨®n es un bonito resultado sobre tri¨¢ngulos que os enuncio a continuaci¨®n:
Dado un tri¨¢ngulo cualquiera, dibujemos tri¨¢ngulos equil¨¢teros apoyados en sus tres lados. Entonces, el tri¨¢ngulo que tiene como v¨¦rtices a sus baricentros tambi¨¦n es equil¨¢tero.
Este teorema se cumple tanto si tomamos los tri¨¢ngulos ¡°exteriores¡± a los lados del tri¨¢ngulo inicial como si tomamos los tri¨¢ngulos ¡°interiores¡±. Y tiene adem¨¢s un interesante a?adido: la diferencia entre el ¨¢rea del tri¨¢ngulo formado por los ¡°v¨¦rtices exteriores¡± y el ¨¢rea del formado por los ¡°v¨¦rtices interiores¡± es igual al ¨¢rea del tri¨¢ngulo inicial. Y todo esto es independiente del tri¨¢ngulo que tomemos inicialmente, se cumple sea cual sea dicho tri¨¢ngulo. En el applet de GeoGebra que ten¨¦is a continuaci¨®n (que tengo colgado en mi perfil de GeoGebraTube) pod¨¦is ver todo esto (moviendo los v¨¦rtices pod¨¦is generar distintos tri¨¢ngulos y ver que el resultado se sigue cumpliendo):
Si os digo la verdad, ser¨ªa magn¨ªfico que este teorema hubiese sido descubierto y demostrado realmente por Napol¨¦on¡pero en realidad esto no es as¨ª. Aunque la demostraci¨®n del mismo no es demasiado complicada, los expertos coinciden en que Napole¨®n no ten¨ªa los conocimientos matem¨¢ticos necesarios para desarrollarla. Y la realidad parece ser que el teorema habr¨ªa que atribu¨ªrselo a Lorenzo Mascheroni, amigo de Napole¨®n (como coment¨¢bamos antes) y gran ge¨®metra. El hecho de que este teorema se haya acabado atribuyendo al emperador se debe a que Napole¨®n era un gran aficionado a los trabajos de Mascheroni, y ello le llev¨® a popularizar sus resultados. Tanto contribuy¨® a dicha popularizaci¨®n que este teorema ha acabado llevando (injustamente) su nombre.
Un baj¨®n, ?verdad? Habr¨ªa estado bien que este consumado estratega militar tambi¨¦n hubiese dedicado parte de su intelecto a demostrar un teorema matem¨¢tico. Pero no, la historia nos ha arruinado una gran historia.
Tenemos que solucionar esto, no podemos acabar el art¨ªculo con este bajonazo. Y para ello os traigo nada menos que a un presidente de los Estados Unidos: James Garfield.
James Garfield fue el vig¨¦simo presidente de los Estados Unidos, aunque por muy poco tiempo: fue elegido en marzo de 1881 y falleci¨® en septiembre del mismo a?o a causa de las heridas provocadas por unos disparos que hab¨ªa recibido poco tiempo antes. En lo que se refiere a sus conocimientos, Garfield ten¨ªa una completa formaci¨®n acad¨¦mica y adem¨¢s era matem¨¢tico aficionado.
?Y cu¨¢l es la relaci¨®n de este presidente con las matem¨¢ticas? Pues muy sencillo: James Garfield desarroll¨® una demostraci¨®n del teorema de Pit¨¢goras, una de las muchas que se conocen, aunque esto no le resta ning¨²n m¨¦rito.
Recordemos el enunciado del teorema de Pit¨¢goras:
En un tri¨¢ngulo rect¨¢ngulo, el cuadrado de la hipotenusa es igual a la suma de los cuadrados de los catetos. Es decir, si h es la hipotenusa del tri¨¢ngulo rect¨¢ngulo y a y b son los catetos del mismo, se cumple que a2+b2=h2.
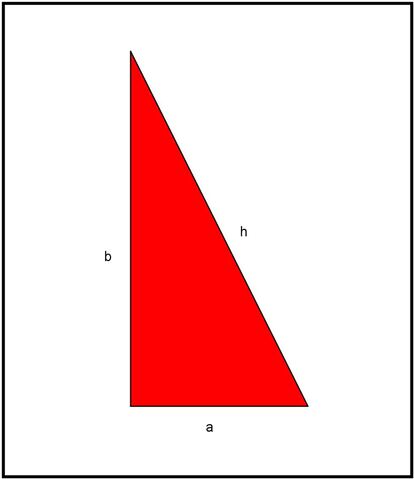
Vamos a ver la demostraci¨®n de Garfield. Partimos de un tri¨¢ngulo rect¨¢ngulo cualquiera, como el de la imagen:
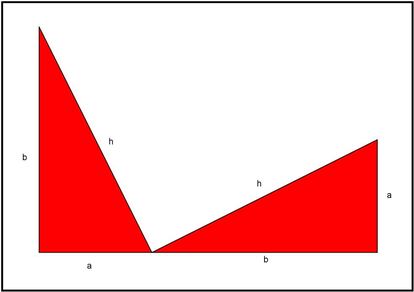
Copiamos el tri¨¢ngulo y los colocamos de manera que el cateto a de uno quede alineado con el cateto b del otro, y que queden pegados por los v¨¦rtices asociados a los dos ¨¢ngulos agudos. La cosa queda de la siguiente forma:
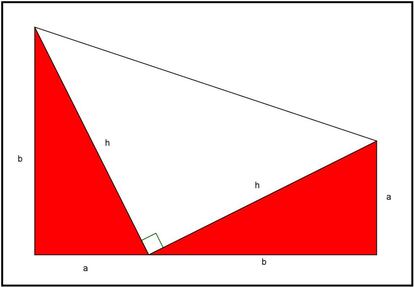
Como los ¨¢ngulos agudos suman 900 y los catetos est¨¢n alineados, el ¨¢ngulo que queda en blanco tambi¨¦n mide 900. Unimos ahora los v¨¦rtices que quedan libres en los dos tri¨¢ngulos, quedan la figura como sigue:
Hemos construido un trapecio, que a su vez est¨¢ dividido en tres tri¨¢ngulos rect¨¢ngulos. Como sabemos calcular el ¨¢rea de un trapecio y tambi¨¦n el ¨¢rea de un tri¨¢ngulo, vamos a calcular el ¨¢rea de la figura completa de dos formas, como trapecio y como uni¨®n de tres tri¨¢ngulos, y despu¨¦s las igualaremos. Aqu¨ª ten¨¦is los c¨¢lculos:
Como trapecio:
El ¨¢rea de un trapecio es igual al producto de la suma de las bases, a y b en este caso (el lado de la izquierda y el de la derecha) multiplicada por la altura, a+b en nuestro trapecio, y dividido todo entre dos. Queda lo siguiente despu¨¦s de desarrollar la expresi¨®n:
Como uni¨®n de tres tri¨¢ngulos rect¨¢ngulos, sabiendo que el ¨¢rea de un tri¨¢ngulo es base por altura dividido todo entre 2:
Igualando las ¨¢reas y cancelando los t¨¦rminos iguales en ambos miembros nos queda lo siguiente:
Vamos, lo que dice el teorema de Pit¨¢goras. Bonita demostraci¨®n, ?verdad?
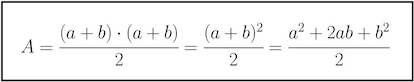
Para finalizar, os pido que si conoc¨¦is alg¨²n caso m¨¢s de dirigente (o persona famosa) que tenga una cierta relaci¨®n con las matem¨¢ticas nos lo dig¨¢is en los comentarios. Seguro que con vuestra ayuda conseguimos una lista de nombres realmente interesante.
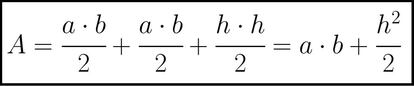
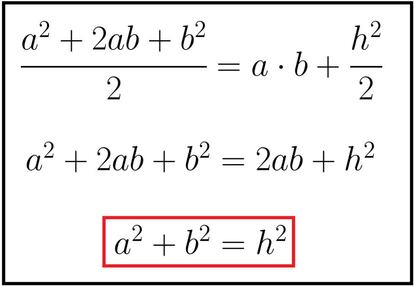
Tu suscripci¨®n se est¨¢ usando en otro dispositivo
?Quieres a?adir otro usuario a tu suscripci¨®n?
Si contin¨²as leyendo en este dispositivo, no se podr¨¢ leer en el otro.
FlechaTu suscripci¨®n se est¨¢ usando en otro dispositivo y solo puedes acceder a EL PA?S desde un dispositivo a la vez.
Si quieres compartir tu cuenta, cambia tu suscripci¨®n a la modalidad Premium, as¨ª podr¨¢s a?adir otro usuario. Cada uno acceder¨¢ con su propia cuenta de email, lo que os permitir¨¢ personalizar vuestra experiencia en EL PA?S.
?Tienes una suscripci¨®n de empresa? Accede aqu¨ª para contratar m¨¢s cuentas.
En el caso de no saber qui¨¦n est¨¢ usando tu cuenta, te recomendamos cambiar tu contrase?a aqu¨ª.
Si decides continuar compartiendo tu cuenta, este mensaje se mostrar¨¢ en tu dispositivo y en el de la otra persona que est¨¢ usando tu cuenta de forma indefinida, afectando a tu experiencia de lectura. Puedes consultar aqu¨ª los t¨¦rminos y condiciones de la suscripci¨®n digital.




























































