Buscando n¨²meros primos con un ¡®peque?o¡¯ teorema

La b¨²squeda de los n¨²meros primos ha sido un tema recurrente en toda la historia de las matem¨¢ticas. Much¨ªsimos han sido (y son) los matem¨¢ticos que han intentado encontrar una regularidad dentro de los n¨²meros primos, una f¨®rmula que siempre devuelva n¨²meros primos o un sistema de detecci¨®n que nos indique si cierto n¨²mero dado es primo o no.

Alguno hay infalible, como la criba de Erat¨®stenes, pero inoperante en la pr¨¢ctica. En este art¨ªculo vamos a intentarlo de otra forma, a ver d¨®nde llegamos.

Vamos a partir del conocido como peque?o teorema de Fermat, formulado por Pierre de Fermat sobre 1636 y demostrado por primera vez por Leonhard Euler en 1736 en su trabajo Theorematum Quorundam ad Numeros Primos Spectantium Demonstratio. Dicho teorema se puede formular de la siguiente forma:

Si p es un n¨²mero primo y a es un n¨²mero entero positivo que no tiene factores comunes con p (es decir, a y p son primos relativos), entonces el resto de la divisi¨®n de a^p-1 entre p es 1. En t¨¦rminos de congruencias, este teorema queda as¨ª:

En principio, este teorema puede ser muy ¨²til para descartar que un n¨²mero es primo, ya que para que un cierto n¨²mero n sea primo es necesario que se cumpla el peque?o teorema de Fermat para todo entero positivo a menor que el propio n.

Veamos un ejemplo. Supongamos que queremos saber si el n¨²mero 413 es primo o no, y vamos a buscar ayuda en el peque?o teorema de Fermat. Tomamos un entero positivo primo relativo con 413, por ejemplo el 2, y aplicamos el test de Fermat. Si 413 fuera primo, tendr¨ªamos que 2^{413 ¨C 1}=2⁴¹² dejar¨ªa de resto 1 al dividirlo entre 413, pero en realidad el resto de esa divisi¨®n es 359. Conclusi¨®n: 413 no es un n¨²mero primo. Os invito a que prob¨¦is con otros n¨²meros y que nos cont¨¦is vuestros resultados.

Probemos ahora con otro n¨²mero. Vamos a tomar uno mucho m¨¢s peque?o para no eternizarnos con las operaciones: el 17. Comencemos tomando a=2 y viendo qu¨¦ nos da la aplicaci¨®n del peque?o teorema de Fermat:

2^17-1=2¹⁶=65536, que al dividirlo entre 17 deja resto 1

Probemos ahora con a=3:

3^17-1=3¹⁶=43046721, cuya divisi¨®n entre 17 nos da, de nuevo, resto 1

Pod¨¦is probar con cualquier otro n¨²mero, ya sea mayor o menor que 17, pero que no tenga factores comunes con ¨¦l (por ejemplo, no valdr¨ªan ni el 51 ni el 85), y en todos los casos obtendr¨¦is resto 1.

?Nos dice esto que 17 es un n¨²mero primo? Pues¡­no, por desgracia no. Lo ¨²nico que nos asegura esto es que no podemos descartar que 17 sea primo¡­

¡­pero sabemos que 17 s¨ª es primo. Si prob¨¢is con cualquier otro n¨²mero primo, tal y como dice el peque?o teorema de Fermat, siempre obtendr¨¦is resto 1 en las divisiones que el teorema dice que hagamos. Por esto, no ser¨ªa descabellado pensar que los primos son los ¨²nicos que cumplen esta propiedad (vamos, que el rec¨ªproco del peque?o teorema de Fermat tambi¨¦n es cierto), pero, ohhhhh, no es as¨ª.

El 561 es el menor n¨²mero compuesto que pasa el test de Fermat. Es, por tanto, el primer n¨²mero de Carmichael.

Hay n¨²meros n que cumplen que, para todo a primo relativo con ellos, las divisiones dan siempre resto 1 sin que dicho n¨²mero n sea primo. Estos n¨²meros se denominan n¨²meros de Carmichael, debido a que fue Robert Carmichael el que encontr¨® el primero de ellos, el 561, en 1910.

Un n¨²mero a que cumple que, para cierto n, la ¡°divisi¨®n de Fermat¡± da resto 1 se llama testigo de Fermat. Este nombre se debe a que el hecho de que esto ocurra nos da como pista que el n¨²mero n podr¨ªa ser primo (aunque no nos lo asegure). Los n¨²meros de Carmichael son n¨²meros compuestos que cumplen que todos los n¨²meros primos relativos con ellos son testigos de Fermat.

Efectivamente, 2⁵⁶⁰ deja resto 1 al dividirlo entre 561; 5⁵⁶⁰ tambi¨¦n deja resto 1 al dividirlo entre 561; y lo mismo pasa para cualquier otro valor de a que sea primo relativo con 561, lo que nos podr¨ªa llevar a pensar que 561 puede ser primo¡­

¡­pero sabemos que no lo es, y se puede ver de una manera muy sencilla: como sus cifras suman 12, que es m¨²ltiplo de 3, tenemos asegurado que 561 es m¨²ltiplo de 3, y por tanto compuesto. Vamos, que es un n¨²mero con apariencia de primo (pasa el ¡°test de Fermat¡±) pero que en realidad no es primo.

Como acabamos de comentar, usar el test de Fermat (o cualquier otro) para sacar alguna conclusi¨®n sobre la primalidad del n¨²mero 561 es una tonter¨ªa, ya que es f¨¢cil y r¨¢pido ver que es un n¨²mero compuesto, pero para otros n¨²meros s¨ª nos puede venir bien para hacernos una idea sobre si son primos o no. Imaginad un n¨²mero n que sea, por ejemplo, producto de dos primos de 50 d¨ªgitos cada uno. Si le pasamos el test de Fermat comenzando con los valores de a m¨¢s peque?os (para que las operaciones sean lo m¨¢s cortas posibles) y obtenemos siempre resto 1, ?qu¨¦ pensar¨ªamos? Pues que es bastante probable que el n¨²mero sea primo, y por eso tiene sentido que se le llame primo probable.

Pero hemos dicho que nuestro n¨²mero es producto de dos n¨²meros primos, y por tanto no es primo. Al ser compuesto, pasa a denominarse pseudoprimo (habr¨ªa que hacer alguna puntualizaci¨®n al respecto de esto ¨²ltimo, pero como no nos hace falta me la salto).

Los n¨²meros de Carmichael, tambi¨¦n llamados pseudoprimos absolutos, deben tener al menos tres factores primos (como, por ejemplo, el 561=3 ¡¤ 11 ¡¤ 17). Vamos, que aunque no puedan tener s¨®lo dos factores estamos en un caso del estilo al comentado antes: son los n¨²meros que hacen que no nos podamos fiar del peque?o teorema de Fermat.

Por cierto, aqu¨ª os dejo un listado con los primeros n¨²meros de Carmichael (secuencia A002997 en la OEIS):

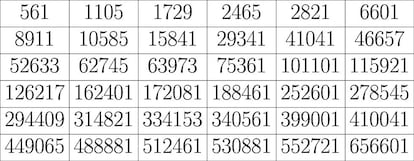
Despu¨¦s de todo lo que hemos comentado, ?para qu¨¦ nos podr¨ªa servir entonces el peque?o teorema de Fermat? Pues, como ya hemos dicho, para detectar primos probables. Har¨ªamos lo siguiente:

- Tomamos el n¨²mero n del que queremos saber si es primo o compuesto

- Le pasamos el test de Fermat con algunos valores de a peque?os (y primos, para no perder el tiempo): 2, 3, 5, 7,¡­

- Si con alguno de ellos obtenemos resto distinto de 1, ya sabemos que nuestro n es compuesto.

- Si obtenemos resto 1 con todos ellos, estamos ante un primo probable. En ese caso, lo mejor es pasar a un test de primalidad m¨¢s completo que el de Fermat, como el test de Miller-Rabin. En la p¨¢gina personal de Ben Lynn ten¨¦is algo m¨¢s de informaci¨®n al respecto.

Para acabar, os dejo algunos datos m¨¢s relacionados con estos interesantes n¨²meros de Carmichael. Son n¨²meros bastantes escasos (por ejemplo, por debajo de 1000000 s¨®lo hay 43 n¨²meros de Carmichael), pero est¨¢n perfectamente caracterizados. Hay un teorema, debido a Alwin Korselt y que data de 1899, que nos da condiciones necesarias y suficientes para que un n¨²mero entero positivos sea un n¨²mero de Carmichael:

Un n¨²mero entero positivo compuesto n es un n¨²mero de Carmichael si y s¨®lo si es libre de cuadrados y para todo divisor primo p de n se cumple que p ¨C 1 es un divisor de n ¨C 1.

(Que un n¨²mero K sea libre de cuadrados significa que no hay ning¨²n n¨²mero primo q tal que q² sea un divisor de K.)

Este teorema caracteriza totalmente a los n¨²meros de Carmichael: si encontramos un n¨²mero compuesto con esas condiciones tenemos asegurado que ser¨¢ un n¨²mero de Carmichael.

Un ¨²ltimo detalle sobre este teorema en el que puede que alguno haya reparado: el teorema de Korselt es anterior a la propia definici¨®n de n¨²mero de Carmichael. Al parecer, Korselt no fue capaz de encontrar ning¨²n n¨²mero con esas caracter¨ªsticas, y hubo que esperar a que Carmichael encontrar el 561 unos a?os despu¨¦s de la aparici¨®n de este teorema.

Por otra parte, tenemos otro interesante teorema, demostrado por Jack Chernick en 1939, que nos proporciona un subconjunto de los n¨²meros de Carmichael. El teorema dice lo siguiente:

Un n¨²mero de la forma (6k+1) ¡¤ (12k+1) ¡¤ (18k+1) es un n¨²mero de Carmichael si sus tres factores son n¨²meros primos (m¨¢s informaci¨®n en On Fermat¡¯s Simple Theorem).

Y, para finalizar, un apunte sobre la cantidad de estos n¨²meros. Como dec¨ªamos, los n¨²meros que citan el teorema de Chernick son solamente algunos de los n¨²meros de Carmichael, y no se sabe cu¨¢ntos hay (si son finitos o infinitos). ?Y qu¨¦ ocurre si hablamos de todos los n¨²meros de Carmichael? Pues que, desde 1994, sabemos que hay infinitos n¨²meros de Carmichael. Lo demostraron Alford, Granville y Pomerance en su trabajo There are infinitely many Carmichael Numbers. Son escasos, y son raros, pero son infinitos.

Como a muchos matem¨¢ticos a lo largo de toda la historia, me fascinan los n¨²meros primos y todo lo que les rodea. Por otra parte, una de mis ¡°debilidades matem¨¢ticas¡± es todo lo que se refiere a Pierre de Fermat. Por ello he querido hablaros sobre este peque?o teorema de Fermat y su relaci¨®n con la b¨²squeda de n¨²meros primos. Adem¨¢s, me ha servido para mostraros estos curiosos n¨²meros de Carmichael y algunas de sus propiedades.

Sobre n¨²meros primos seguiremos hablando. Y, sobre ellos, me gustar¨ªa que propusierais en los comentarios temas relacionados con ellos que puedan ser susceptibles de ser tratados en este blog. Muchas gracias.