?Cu¨¢l es el siguiente t¨¦rmino?

Internet est¨¢ repleto de p¨¢ginas en las que nos proponen problemas relacionados con secuencias l¨®gicas. Sab¨¦is a qu¨¦ me refiero, ?verdad? S¨ª, esas secuencias en las que nos dan algunos t¨¦rminos y nos piden que, de manera l¨®gica, ¡°adivinemos¡± el siguiente.

Podemos encontrar problemas de secuencias l¨®gicas de muchos tipos, como los relacionados con s¨ªmbolos (nos dan una serie de s¨ªmbolos colocados en distintas posiciones o coloreados de diferentes formas y nos piden que adivinemos el siguiente) o relojes (nos dan unos cuantos relojes con horas distintas y nos proponen que digamos cu¨¢l ser¨ªa el que contin¨²a la serie), pero los m¨¢s comunes (y, posiblemente, los que dan m¨¢s juego) son los problemas relacionados con secuencias num¨¦ricas.

Vamos a ver alg¨²n ejemplo. Imaginaos que os propongo que continu¨¦is la siguiente secuencia num¨¦rica:

1, 2, 3, 4, 5,¡­

Posiblemente elegir¨ªais como siguiente t¨¦rmino al n¨²mero 6. Sencillo, ?verdad? Veamos otro ejemplo:

3, 5, 7,¡­

Aqu¨ª ya se nos podr¨ªan ocurrir m¨¢s cosas sin necesidad de pensar demasiado. Podr¨ªamos imaginar que la secuencia corresponde con los n¨²meros impares a partir del 3, por lo que el siguiente t¨¦rmino ser¨ªa el 9. Pero tambi¨¦n tendr¨ªa sentido que la secuencia fuera la que nos muestra los n¨²meros primos impares, por lo que deber¨ªa seguir con el n¨²mero 11. Ambas respuestas ser¨ªan correctas, y bastante razonables.

Y un ejemplo m¨¢s. A ver qui¨¦n puede seguir la siguiente secuencia:

2, 10, 12, 16, 17, 18, 19,...

?Cu¨¢l ser¨ªa el siguiente t¨¦rmino? Os dejo que pens¨¦is y que nos cont¨¦is vuestros progresos en los comentarios (si alguien conoc¨ªa la serie y, por tanto, ya sab¨ªa la respuesta que se espere un poco para comentarlo para dejar as¨ª que la gente piense).

Volvamos a la secuencia 3, 5, 7. Hemos dicho que tendr¨ªa sentido seguirla con un 9 (n¨²meros impares a partir del 3) o con el 11 (n¨²mero primos impares). ?S¨®lo con esos? ?Se podr¨ªa seguir con el n¨²mero 14? ?Tendr¨ªa sentido que el siguiente t¨¦rmino fuera el 47? ?Y el 1111? Pues el caso es que s¨ª, tendr¨ªa sentido continuar esa secuencia con cualquier n¨²mero que se nos ocurra, entendiendo ¡°tener sentido¡± como que para cualquier n¨²mero K podr¨ªamos encontrar una regla a partir de la cual obtenemos el 3, luego el 5, despu¨¦s el 7 y a continuaci¨®n el n¨²mero K elegido.

Esto est¨¢ demostrado, y adem¨¢s desde hace ya tiempo. En 1795, Joseph Louis Lagrange publicaba un resultado que est¨¢ muy relacionado con estas secuencias num¨¦ricas. Dicho resultado (que, por cierto, hab¨ªa sido descubierto por Edward Waring en 1779) dice b¨¢sicamente que para cualquier secuencia de n¨²meros podemos encontrar una regla (m¨¢s concretamente, un polinomio) que para los valores 1, 2, 3, etc, nos da los t¨¦rminos de dicha secuencia.

Dicho polinomio, llamado polinomio interpolador, se calcula a partir de los t¨¦rminos de la propia secuencia. Podr¨ªamos entonces a?adir el n¨²mero que quisi¨¦ramos y despu¨¦s calcular el polinomio interpolador de la secuencia obtenida, obteniendo as¨ª la ¡°regla¡± que explica el porqu¨¦ de nuestra elecci¨®n. No tiene por qu¨¦ ser una regla sencilla, lo interesante es que la hay. Aqu¨ª os dejo las reglas que explicar¨ªan las elecciones 9, 11, 14, 47 y 1111 para la secuencia 3, 5, 7:

Alguno de vosotros pensar¨¦is que con esto le acabamos de quitar toda la gracia a la b¨²squeda de reglas que expliquen una elecci¨®n concreta del siguiente t¨¦rmino de una secuencia num¨¦rica. Por ejemplo, para la secuencia

1, 2, 4, 8, 16,¡­

seguro que la mayor¨ªa (posiblemente todos) habr¨ªais contestado que el siguiente t¨¦rmino es el 32, al ser la siguiente potencia de 2 (la secuencia propuesta es 2⁰, 2¹, 2², 2³, 2⁴). Pero con lo que hemos comentado antes ya sabemos que para cualquier n¨²mero que eligi¨¦ramos podr¨ªamos encontrar una regla que le diera sentido.

Ahora, eso no significa que no podamos encontrar relaciones curiosas y bellas que expliquen ciertas elecciones ¡°no habituales¡±. Por ejemplo, ?y si os digo que busqu¨¦is alguna regla curiosa o interesante que explique que la elecci¨®n del siguiente t¨¦rmino de la secuencia fuera el 31?

Si, vale, elegimos el 31, calculamos el polinomio interpolador y ya tenemos la regla. Pero, en este caso, existe una bonita explicaci¨®n para esta elecci¨®n. Tomamos una circunferencia, elegimos puntos sobre ella y los unimos con segmentos de todas las formas posibles (cuid¨¢ndonos de que no haya tres segmentos que se corten en un punto). Hemos esto, contamos el n¨²mero de regiones en las que ha quedado dividido el c¨ªrculo interior a dicha circunferencia.

Comenzamos tomando un punto nada m¨¢s. En este caso no se puede trazar ning¨²n segmento (necesitamos al menos dos puntos), por lo que nos queda una ¨²nica regi¨®n (el c¨ªrculo completo). Tenemos entonces que el primer t¨¦rmino de la secuencia es 1.

Tomemos ahora dos puntos. Ahora podemos trazar un ¨²nico segmento, que divide al c¨ªrculo en dos regiones. Entonces, el segundo t¨¦rmino de la secuencia es 2.

Vamos ahora con tres puntos. Aqu¨ª podemos trazar tres segmentos, que dejan dividido el c¨ªrculo en exactamente cuatro regiones. Por tanto, el tercer t¨¦rmino de la secuencia es 4. En la siguiente imagen pod¨¦is ver estos tres primeros casos:

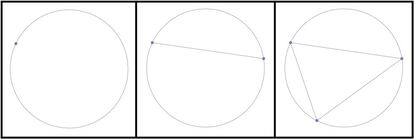
Con cuatro puntos se pueden trazar seis segmentos, que dividen el c¨ªrculo en ocho regiones, y con cinco puntos podemos trazar diez segmentos, quedando el c¨ªrculo dividido en diecis¨¦is partes. Entonces, los siguientes t¨¦rminos de la secuencia son, efectivamente, 8 y 16. A continuaci¨®n, pod¨¦is ver las dos situaciones:

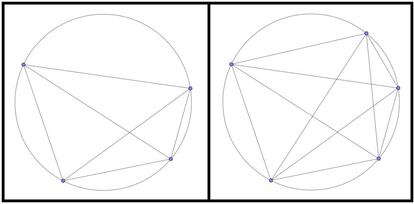
Y vayamos ahora al caso de seis puntos, el que corresponde al t¨¦rmino que nos preguntaban. Unimos esos seis puntos de la forma comentada y contamos regiones. Pod¨¦is hacer vosotros mismos el dibujo, pero por si acaso no ten¨¦is papel y boli a mano (bueno, o por si no ten¨¦is muchas ganas de hacer dibujitos) os lo dejo yo hecho. Contad:

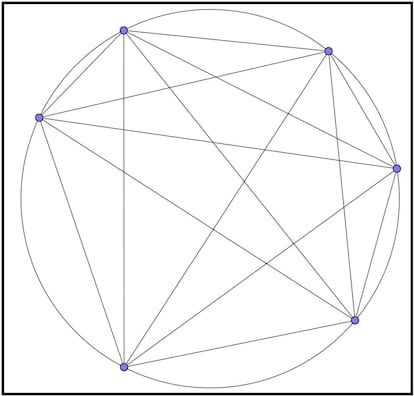
Exacto, el c¨ªrculo interior queda dividido en 31 regiones exactamente. Tenemos entonces una secuencia que coincide con las potencias de 2 en los primeros cinco t¨¦rminos pero que difiere en el sexto. Y no s¨®lo en este, sino que a partir de ah¨ª las diferencias van siendo cada vez m¨¢s grandes: 57 (frente a 64), 99 (frente a 128), etc. La regla (el polinomio) que nos calcula exactamente el n¨²mero de regiones en las que queda dividido el c¨ªrculo interior actuando de la forma descrita es la siguiente:

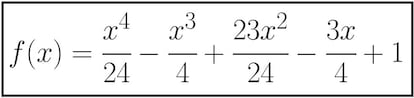
No creo que pod¨¢is negar lo curioso de este problema de las regiones y, por qu¨¦ no decirlo, la belleza que contiene.

Muy interesante esto de las secuencias num¨¦ricas, un mundo en el que podemos encontrar todo tipo de situaciones curiosas y en el que nos podemos llevar muchas sorpresas. Para finalizar este art¨ªculo, os quiero proponer otra secuencia que, aunque es ciertamente conocida, no deja de tener inter¨¦s. Es la siguiente:

1, 11, 21, 1211, 111221, 312211,¡­

Os invito a que pens¨¦is cu¨¢l ser¨ªa el siguiente t¨¦rmino de la serie, dando una regla que nos indique c¨®mo encontrar los siguientes. Os pido, igual que antes, que si ya la conoc¨¦is no le fastidi¨¦is el entretenimiento a quien quiera pensar. Dejad un rato para que la gente piense y, si pasa un tiempo y nadie lo dice, comentad la soluci¨®n. Muchas gracias.