?C¨®mo sabe el GPS qu¨¦ ruta recomendarnos?

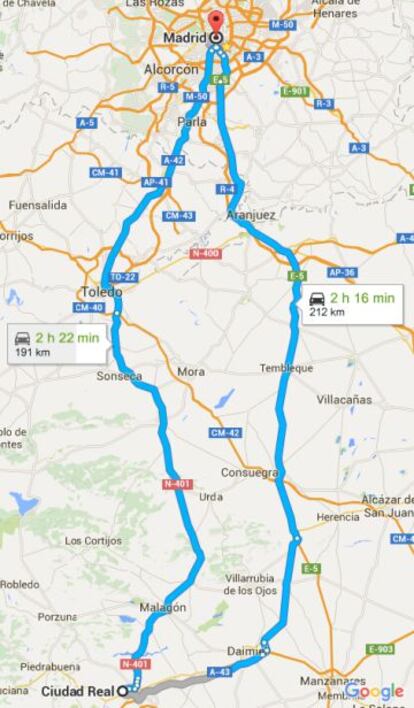
Vivo en Ciudad Real, pero tengo mucha familia en Madrid. Un tema recurrente, desde hace m¨¢s de treinta y cinco a?os, cuando llegan o llegamos de viaje, es si hemos ido o venido por la carretera de Toledo o por la de Andaluc¨ªa. A diferencia del GPS al que podr¨ªamos consultar para ver qu¨¦ camino es mejor, nosotros tenemos mucha experiencia en este recorrido (y en la conversaci¨®n consiguiente).

El inexperto aparato, sin embargo, recomienda uno u otro camino en funci¨®n de la distancia, de las caracter¨ªsticas de cada carretera, e incluso de las horas en que preveamos viajar: as¨ª, el sistema inform¨¢tico de enrutamiento puede mostrarnos una alternativa u otra. Lo que no har¨¢, seguro, es recomendarnos pasar por Badajoz, o por Valencia, o por C¨¢diz, para llegar desde nuestro origen, en mitad de La Mancha, hasta la capital, en el centro de la Pen¨ªnsula Ib¨¦rica.

La determinaci¨®n del camino m¨ªnimo desde un lugar de origen a uno de destino es un problema cl¨¢sico en Inform¨¢tica, que cualquier estudiante universitario de esta disciplina debe saber resolver.

El problema responde a lo que se llama un recorrido en un grafo que, en Inform¨¢tica, es un colecci¨®n de puntos (ciudades o edificios o direcciones postales, por ejemplo) con l¨ªneas que los conectan (carreteras, calles, caminos). A cada l¨ªnea se le asigna lo que se llama un "peso", que normalmente es la distancia, pero que puede ser otro factor (como el n¨²mero de carriles o la velocidad m¨¢xima permitida) o una conjunci¨®n de factores (la distancia y el n¨²mero de carriles y la velocidad m¨¢xima y la existencia de obras en alg¨²n trecho).

La determinaci¨®n del camino m¨ªnimo desde un lugar de origen a uno de destino es un problema cl¨¢sico en Inform¨¢tica, que cualquier estudiante universitario de esta disciplina debe saber resolver

?C¨®mo determina un sistema inform¨¢tico la ruta ¨®ptima de manera autom¨¢tica? El c¨¢lculo del camino ¨®ptimo es lo que se llama un problema de orden n², es decir, que su tiempo de c¨¢lculo depende del n¨²mero de puntos en el mapa elevado al cuadrado. Pero son tantos los puntos en el mapa (s¨®lo Espa?a tiene m¨¢s de 8.000 municipios, cada uno con sus calles, cruces, monumentos, edificios p¨²blicos¡­) que la aplicaci¨®n del llamado algoritmo de Dijkstra se torna imposible.

Para resolver este tipo de problemas en un tiempo razonable se utilizan algoritmos que se llaman "voraces": un algoritmo voraz avanza progresivamente hacia la soluci¨®n, en varios pasos, tomando en cada paso el trozo "m¨¢s gordo" de la tarta o, en nuestro contexto, el elemento de la soluci¨®n que abarata m¨¢s, al menos parcialmente, el recorrido entre los dos puntos.

En el caso concreto de la determinaci¨®n del camino m¨ªnimo en un mapa se utiliza habitualmente un algoritmo llamado A* ("A asterisco" o "A estrella"), que mezcla la heur¨ªstica humana (es decir: c¨®mo ir¨ªamos de Madrid a Ciudad Real si no tuvi¨¦ramos GPS) con el rigor matem¨¢tico y el pseudorigor voraz. En efecto, A* considera todos los lugares a los que podemos llegar directamente desde el lugar origen y calcula la distancia a cada uno: por ejemplo, para llegar de Madrid a Ciudad Real, calcula primero la distancia desde Madrid a sus lugares directamente adyacentes: Alcorc¨®n (16 km), Las Rozas (19), Parla (25) o Alcal¨¢ de Henares (35,6); hecho esto, determina la distancia en l¨ªnea recta desde cada uno de estos lugares intermedios hasta el lugar de destino: 150 km desde Alcorc¨®n, 167 desde Las Rozas, 136 desde Parla, 172 desde Alcal¨¢, y suma las dos distancias: 166 Madrid-Ciudad Real si vamos por Alcorc¨®n; 183 por Las Rozas; 161 si pasamos por Parla; 197 desvi¨¢ndonos por Alcal¨¢.

Para resolver este tipo de problemas en un tiempo razonable se utilizan algoritmos que se llaman "voraces": un algoritmo voraz avanza progresivamente hacia la soluci¨®n, en varios pasos, tomando en cada paso el trozo 'm¨¢s gordo' de la tarta

As¨ª que A* se queda con Parla, descarta los dem¨¢s municipios y repite el proceso: ?A d¨®nde podemos ir desde Parla? A Getafe, a Pinto, a Fuenlabrada, a Illescas. ?Qu¨¦ distancias hay desde Parla a estos sitios? ?Y qu¨¦ distancia en l¨ªnea recta desde estos sitios a Ciudad Real, nuestro destino? Pues A* hace lo mismo: calcula, suma y selecciona; calcula, suma y selecciona; calcula de nuevo, suma otra vez y selecciona un nuevo subobjetivo; e itera as¨ª, hasta que consigue al fin recomendarnos las dos rutas, Toledo y Andaluc¨ªa, sin ser capaz tampoco la Inform¨¢tica y sus m¨¦todos de c¨®mputo de resolvernos esa duda que nos corroe a mi familia y a m¨ª desde hace ya tantos a?os.

Macario Polo Usaola es profesor titular de la Universidad de Castilla-La Mancha (¨¢rea de Lenguajes y Sistemas Inform¨¢ticos), en el campus de Ciudad Real.

Cr¨®nicas del Intangible es un espacio de divulgaci¨®n sobre las ciencias de la computaci¨®n, coordinado por la sociedad acad¨¦mica SISTEDES (Sociedad de Desarrollo de Ingenier¨ªa y de Tecnolog¨ªas de Desarrollo de Software). El intangible es la parte no material de los sistemas inform¨¢ticos (es decir, el software), y aqu¨ª se relatan su historia y su devenir. Los autores son profesores de las universidades espa?olas, coordinados por Ricardo Pe?a Mar¨ª (catedr¨¢tico de la Universidad Complutense de Madrid) y Macario Polo Usaola (profesor titular de la Universidad de Castilla-La Mancha.