Tromin¨®s

La partida m¨¢s corta posible de ¡°brotes¡±, el juego inventado por Conway del que habl¨¢bamos la semana pasada, es la partida trivial en la que se parte de un solo brote: el primer jugador lo une consigo mismo mediante un trazo circular y marca un nuevo brote en dicho trazo; el segundo jugador une los dos brotes y gana, ya que de este modo los ¡°mata¡± ambos y no se puede trazar una nueva ¡°rama¡±.

Vimos que con 2 brotes iniciales tambi¨¦n gana siempre el segundo jugador, as¨ª como con 6, 7 u 8, mientras que hay una estrategia ganadora para el primer jugador cuando se parte de 3, 4, 5, 9, 10 u 11 brotes. Pero no hay, o no se conoce, una pauta regular en la distribuci¨®n de estrategias ganadoras en funci¨®n del n¨²mero de brotes iniciales.

Todas las partidas de brotes terminan en un n¨²mero de jugadas comprendido entre 2n y 3n ¨C 1, siendo n el n¨²mero de brotes iniciales; as¨ª, la partida elemental analizada en las ¨²ltimas semanas, a partir de 2 brotes iniciales, puede terminar en 4 jugadas, como vimos, si el segundo jugador sigue la estrategia ¨®ptima, y puede llegar a 5 jugadas si no hace (invito a mis sagaces lectoras/es a comprobarlo¡­ o desmentirlo).

En cuanto a la secuencia 1, 1, 2, 3, 5, 8, 10, 13¡­, vinculada a la secuencia mira-y-di de Conway, ser¨ªa la de Fibonacci si no fuera por ese 10 intercalado entre el 8 y el 13. Los siguientes t¨¦rminos son 16 y 23. ?Por qu¨¦?

Del domin¨® al tromin¨®

Y tras el peque?o homenaje de las ¨²ltimas semanas al gran John Horton Conway, fallecido el pasado 11 de abril a causa de la covid-19, podemos retomar -con la intenci¨®n de generalizarlo- el asunto de las fichas de domin¨® y los tatamis -es decir, los rect¨¢ngulos de 2 x 1- y su forma de recubrir el plano.

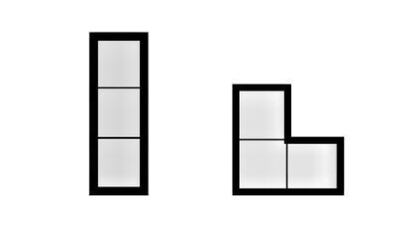
Si a un domin¨® le pegamos un tercer cuadrado que comparta un lado con uno de sus dos cuadrados, obtenemos un ¡°tromin¨®¡±. Solo hay dos maneras sustancialmente distintas -es decir, considerando iguales las que se obtienen unas de otras por rotaci¨®n- de pegarle un tercer cuadrado a un domin¨®: formando una hilera de tres cuadrados, denominado tromin¨® I, o formando un ¨¢ngulo recto, denominado tromin¨® L o V.

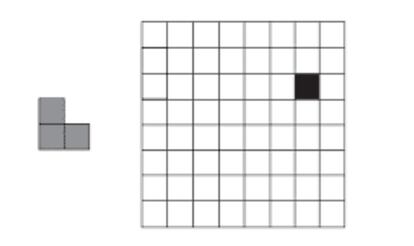
Puesto que el tablero de ajedrez tiene 64 casillas, es evidente que no podemos recubrirlo por completo con tromin¨®s, ya que 64 no es divisible por 3. Pero si le quitamos al tablero una casilla, 63 s¨ª es m¨²ltiplo de 3. ?Se puede recubrir el tablero ¡°mutilado¡± de la figura con 21 tromin¨®s L? ?Y con 21 tromin¨®s I? ?Siempre ser¨¢n posibles tales recubrimientos, cualquiera que sea la casilla del tablero eliminada?

Es f¨¢cil ver que ambos tromin¨®s, el I y el L, pueden descomponerse en n2 tromin¨®s del mismo tipo, siendo n cualquier n¨²mero natural; por lo tanto, los tromin¨®s son rep-tiles, un juego de palabras en ingles que significa ¡°teselas repetitivas¡±.

Hay un viejo acertijo geom¨¦trico que ilustra la ¨ªndole ¡°reptiliana¡± de los tromin¨®s:

Un campesino tiene un terreno cuadrado que divide en cuatro cuadrados iguales; se reserva uno de los cuartos para ¨¦l y los otros tres cuartos se los cede a sus cuatro hijos, con la condici¨®n de que hagan cuatro parcelas iguales en forma y tama?o. ?C¨®mo lo hacen?

Carlo Frabetti es escritor y matem¨¢tico, miembro de la Academia de Ciencias de Nueva York. Ha publicado m¨¢s de 50 obras de divulgaci¨®n cient¨ªfica para adultos, ni?os y j¨®venes, entre ellos Maldita f¨ªsica, Malditas matem¨¢ticas o El gran juego. Fue guionista de La bola de cristal.

Puedes seguir a Materia en Facebook, Twitter, Instagram o suscribirte aqu¨ª a nuestra newsletter.