Mira y di

En la breve partida de Brotes (o Juego del drago) planteada la semana pasada, la cuarta jugada puede ser la ¨²ltima, como muestra la figura. No es posible trazar una nueva ¡°rama¡± que cumpla las reglas del juego, puesto que de un mismo brote no pueden salir m¨¢s de tres ramas; todos los brotes menos dos ya est¨¢n ¡°muertos¡±, que es como se denominan cuando alcanzan las tres ramas, y los dos brotes ¡°vivos¡± no pueden conectarse entre s¨ª sin cortar otra rama, lo cual tampoco est¨¢ permitido.

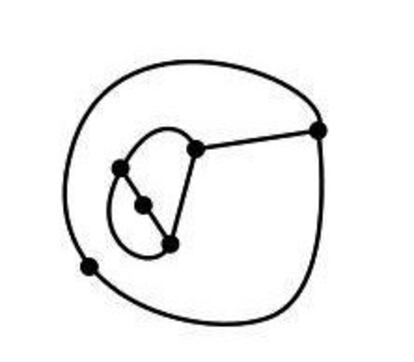
As¨ª pues, partiendo de 2 brotes se puede acabar la partida en 4 jugadas. ?Puede haber una partida a¨²n m¨¢s corta?

En la minipartida examinada, hemos visto que ha ganado el que juega en segundo lugar, y se puede demostrar que siempre hay una estrategia ganadora para el segundo jugador si se parte de 2, 6, 7 u 8 brotes. Sin embargo, si se parte de 3, 4, 5, 9, 10 u 11 brotes, siempre hay una estrategia ganadora para el primer jugador. ?Hay alguna pauta en este reparto de estrategias ganadoras?

Es evidente que en una partida finita no puede haber empate, ya que ha de haber una ¨²ltima jugada, y por ende un ganador; pero ?puede haber partidas interminables, o hay un l¨ªmite superior e inferior para el n¨²mero de jugadas en funci¨®n del n¨²mero inicial de brotes?

Desintegraci¨®n audioactiva

En su d¨ªa hablamos de la curiosa secuencia mira-y-di de Conway, en la que cada t¨¦rmino es la ¡°descripci¨®n¡± esquem¨¢tica del anterior:

1, 11 (un uno), 21 (dos unos), 1211 (un dos, un uno), 111221 (un uno, un dos, dos unos), 312211 (tres unos, dos doses, un uno), 13112221¡­

El n¨²mero inicial puede ser cualquiera, excepto el 22, que da lugar a una sucesi¨®n degenerada, la repetici¨®n sin fin del n¨²mero de partida: 22, 22 (dos doses), 22¡­ E independientemente del t¨¦rmino inicial, el cociente entre el n¨²mero de cifras de un t¨¦rmino y el del t¨¦rmino anterior tiende a una cantidad fija, la constante de Conway: 1.303577¡­, un n¨²mero algebraico que es la ¨²nica soluci¨®n positiva de una ecuaci¨®n de 71? grado.

A partir de un cierto punto, la mayor¨ªa de los t¨¦rminos de la sucesi¨®n pueden descomponerse en secuencias menores que se repiten y recombinan para formar los sucesivos t¨¦rminos; estos bloques recurrentes son 92, y Conway los llam¨® ¡°elementos¡± por el paralelismo con los de la tabla peri¨®dica; de ah¨ª el jocoso nombre de ¡°desintegraci¨®n audioactiva¡± (en vez de radiactiva), pues, a partir de un cierto punto, casi todos los t¨¦rminos pueden descomponerse en varios de estos 92 bloques b¨¢sicos. Invito a mis sagaces lectoras/es a descubrir y manejar algunos de estos ¡°elementos¡± (como era de esperar en funci¨®n de lo visto anteriormente, el m¨¢s simple y recurrente de estos bloques es el 22, al que, por esta raz¨®n, Conway denomin¨® ¡°hidr¨®geno¡±).

Y un homenaje al gran Conway, maestro de juegos y jugadores, no puede terminar sin un acertijo ad hoc basado en mira-y-di:

Hallar el siguiente t¨¦rmino de la secuencia 1, 2, 3, 5, 8, 10, 13¡­

Carlo Frabetti es escritor y matem¨¢tico, miembro de la Academia de Ciencias de Nueva York. Ha publicado m¨¢s de 50 obras de divulgaci¨®n cient¨ªfica para adultos, ni?os y j¨®venes, entre ellos Maldita f¨ªsica, Malditas matem¨¢ticas o El gran juego. Fue guionista de La bola de cristal.

Puedes seguir a Materia en Facebook, Twitter, Instagram o suscribirte aqu¨ª a nuestra newsletter.