Poliformas

Adem¨¢s del oscilador R, equivalente al pentomin¨® F, nos pregunt¨¢bamos la semana pasada qu¨¦ otros patrones t¨ªpicos del juego de la vida se corresponden con poliomin¨®s. Tal vez el caso m¨¢s claro sea el tetromin¨® O, que en el juego de la vida es una ¡°vida est¨¢tica¡± (?por qu¨¦ se denomina as¨ª?).

Como era de prever, el n¨²mero de poliomin¨®s crece r¨¢pidamente al aumentar el n¨²mero de cuadrados. Hay 1 domin¨®, 2 tromin¨®s, 5 tetromin¨®s, 12 pentomin¨®s, 35 hexomin¨®s, 108 heptomin¨®s y 369 octomin¨®s, y la secuencia sigue creciendo a un ritmo irregular pero pr¨®ximo al de una progresi¨®n geom¨¦trica de raz¨®n 3:

1, 2, 5, 12, 35, 108, 369, 1.285, 4.655, 17.073, 63.600¡­

Los 35 hexomin¨®s suman un total de 210 cuadrados, por lo que, en principio, se podr¨ªa formar con ellos un rect¨¢ngulo de 14 x 15, 10 x 21, 7 x 30, 6 x 35 o 5 x 42. Pero solo en principio, pues ninguna de estas construcciones es posible, como se puede ver aplicando el mismo criterio de paridad al que hemos recurrido en otros casos contemplados recientemente:

Efectivamente, si en cualquiera de los rect¨¢ngulos anteriores coloreamos los cuadrados alternativamente de blanco y negro, como en un tablero de ajedrez, tendremos, obviamente, el mismo n¨²mero de casillas blancas y negras: 105 de cada. Pero si hacemos lo mismo con los hexomin¨®s, vemos que en 11 de ellos hay un n¨²mero par de cuadrados de cada color (2 blancos y 4 negros o viceversa) y en 14 de ellos hay un n¨²mero impar de cada color (3 blancos y 3 negros); por lo tanto, los hexomin¨®s sumar¨¢n, en total, un n¨²mero par de cuadrados blancos y un n¨²mero par de negros, por lo que no podr¨¢n formar un rect¨¢ngulo en el que ha de haber 105 de cada color.

S¨ª que es posible, sin embargo, componer elegantes rect¨¢ngulos y cuadrados ¡°agujereados¡± como el de la figura.

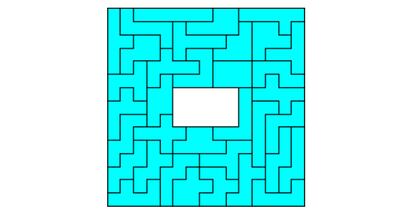
De los 35 hexomin¨®s, 11 son desarrollos planos del cubo. Mis sagaces lectoras/es pueden entretenerse dobl¨¢ndolos mentalmente.

Como vimos, hay un solo heptomin¨® con agujero, a partir del cual podemos obtener 6 octomin¨®s con agujero distintos. El m¨¢s obvio y regular es la cuadr¨ªcula de 3 x 3 sin el cuadrado central.

Polidiamantes y otras poliformas

Generalizando el concepto de domin¨® a un n¨²mero cualquiera de cuadrados adyacentes, se obtienen los poliomin¨®s: tromin¨®s, tetromin¨®s, pentomin¨®s¡­ Pero, a su vez, el concepto de poliomin¨® se puede ampliar a todo tipo de pol¨ªgonos.

Especial inter¨¦s revisten las poliformas de pol¨ªgonos regulares. Adem¨¢s de los poliomin¨®s, cuya ¡°c¨¦lula¡±, como hemos visto es el cuadrado, las m¨¢s destacadas son los polidiamantes (llamados as¨ª porque dos tri¨¢ngulos equil¨¢teros que comparten un lado forman el consabido ¡°diamante¡± de la baraja inglesa) y los polihex, integrados, respectivamente, por tri¨¢ngulos equil¨¢teros y hex¨¢gonos regulares, que comparten con el cuadrado una singular propiedad en lo que a la acumulaci¨®n ¡°polif¨®rmica¡± se refiere (?cu¨¢l es esa propiedad que solo estos tres pol¨ªgonos regulares poseen?).

La versatilidad de los tri¨¢ngulos equil¨¢teros es menor, obviamente, que la de los cuadrados; solo hay 1 tridiamante y 3 tetradiamante. ?Cu¨¢ntos pentadiamantes hay? ?Y hexadiamantes?

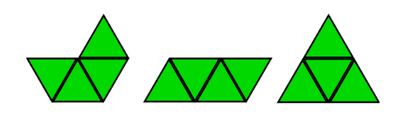
Invito a mis sagaces lectoras/es a explorar el inagotable mundo de las poliformas en busca de secuencias y singularidades.

Carlo Frabetti es escritor y matem¨¢tico, miembro de la Academia de Ciencias de Nueva York. Ha publicado m¨¢s de 50 obras de divulgaci¨®n cient¨ªfica para adultos, ni?os y j¨®venes, entre ellos ¡®Maldita f¨ªsica¡¯, ¡®Malditas matem¨¢ticas¡¯ o ¡®El gran juego¡¯. Fue guionista de ¡®La bola de cristal¡¯.

Puedes seguir a Materia en Facebook, Twitter, Instagram o suscribirte aqu¨ª a nuestra newsletter