C¨®mo visitar dos millones de estrellas en el menor tiempo posible

El proyecto Gaia de la Agencia Espacial Europea tiene 2.079.471 estrellas catalogadas. ?Podr¨ªamos encontrar una ruta para visitarlas todas, en el menor tiempo posible? Recientemente, un grupo de investigadores ha dado con un camino que se acerca mucho a la respuesta. Este tipo de cuestiones se estudian en un ¨¢rea de las matem¨¢ticas conocida como optimizaci¨®n matem¨¢tica o programaci¨®n matem¨¢tica, de gran importancia no s¨®lo te¨®rica sino tambi¨¦n por sus aplicaciones a la vida real y por sus ramificaciones en otras disciplinas.

Se trata de identificar, entre todas las posibilidades para resolver un problema, la mejor, respecto a un criterio establecido. Nos hacemos este tipo de preguntas cuando elegimos compa?¨ªa telef¨®nica ¨Cqueremos elegir la que nos ofrezca un servicio m¨¢s adecuado a un precio m¨¢s bajo¨C, cuando vamos a hacer recados por nuestro barrio ¨Cqueremos desplazarnos gastando la menor energ¨ªa y tiempo posible¨C o al planificar un largo paseo por el universo. En todos los casos, escogemos entre todas las posibilidades existentes ¨Cel conjunto de compa?¨ªas telef¨®nicas, las diversas rutas por nuestro barrio o por el cosmos¨C para optimizar una cantidad ¨Cdinero o tiempo¨C.

El problema del paseo estelar es un ejemplo del problema del viajante de comercio (del ingl¨¦s travelling salesmen problem), uno de los m¨¢s importantes del campo. Se parte de una red de ciudades, interconectadas entre ellas por carreteras. A partir de ella definimos un grafo, es decir, una estructura matem¨¢tica abstracta que contiene objetos ¨Clos v¨¦rtices del grafo y relaciones entre los mismos ¨Clas aristas del grafo¨C. En nuestro caso, los v¨¦rtices ser¨ªan las ciudades y habr¨ªa una arista entre dos ciudades si estas se encuentran conectadas por una carretera. Adem¨¢s, incluiremos la distancia existente entre las ciudades conectadas dando un peso a las aristas, es decir, un valor que se corresponde a los kil¨®metros de separaci¨®n.

El problema del paseo estelar es un ejemplo del problema del viajante de comercio, uno de los m¨¢s importantes del campo

Ahora, un viajante busca la manera de visitar todas las ciudades sin repetici¨®n, acabando el recorrido en la ciudad inicial y utilizando el menor n¨²mero posible de kil¨®metros. En lenguaje matem¨¢tico, la cuesti¨®n consiste en encontrar lo que se denomina un ciclo ¨Cun grafo que empieza y acaba en el mismo punto¨C hamiltoniano ¨Cque solo pasa una vez por cada v¨¦rtice¨C en el grafo bajo estudio, de tal forma que la suma de pesos de sus aristas sea el m¨¢s peque?o posible.

Para un n¨²mero peque?o de ciudades la cuenta la podemos hacer a mano, pero la complejidad del problema aumenta r¨¢pidamente en funci¨®n de las ciudades que estemos considerando. Tomando m¨¢s de 20 ciudades y suponiendo que el n¨²mero de conexiones es elevado ¨Cel n¨²mero m¨¢ximo de carreteras en este caso ser¨ªa 190, en el supuesto que hubiera una carretera directa entre cualquier par de localidades¨C, el problema algor¨ªtmico de calcular todas las rutas se convierte en una cuesti¨®n intratable. De hecho, es bien conocido que se trata de un problema algor¨ªtmico dif¨ªcil: encontrar la soluci¨®n, incluso utilizando ordenadores potentes, necesita de tanto tiempo de c¨¢lculo que se considera impracticable.

Sin embargo, los m¨¦todos modernos permiten encontrar soluciones casi-¨®ptimas en tiempos de c¨¢lculo razonables. Estas son soluciones del problema que no minimizan el n¨²mero de kil¨®metros, pero que se acercan mucho a ello, es decir, su diferencia con respecto al ¨®ptimo es peque?a. En dicha b¨²squeda se utilizan una ¨¢mplia variedad de t¨¦cnicas matem¨¢ticas, que incluyen el uso de heur¨ªsticas, la estad¨ªstica, la probabilidad y el an¨¢lisis.

El estudio de este problema motiv¨® el desarrollo de muchas de las ideas centrales en esta disciplina. El trabajo fundamental, del a?o 1954, es Solution of a large-scale travelling-sales problem. En ¨¦l, George Dantzig ¨Cpadre del algoritmo¨C, Delbert R. Fulkerson y Selmer Johnson pusieron los cimientos al estudio formal del problema del viajante y, de paso, dieron forma a toda la disciplina de la programaci¨®n matem¨¢tica (que ya recibi¨® un gran impulso durante la II Guerra Mundial). Como dato curioso, los autores estudiaron el problema para 48 ciudades de Estados Unidos, y obtuvieron una ruta para visitarlas a todas siguiendo un ciclo hamiltoniano.

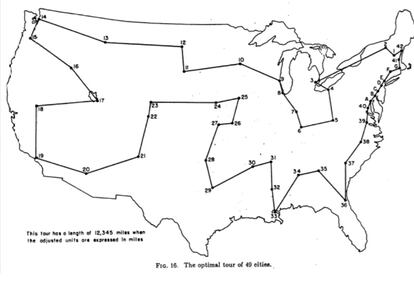
Actualmente y gracias a la potencia algor¨ªtmica de los computadores, se pueden estudiar sistemas much¨ªsimo m¨¢s complejos que en los a?os cincuenta y, sorprendentemente, obtener resultados muy cercanos al valor ¨®ptimo. Es el caso del reciente trabajo de Bill Cook (Universidad de Waterloo, Canad¨¢) y Keld Helsgaun (Universidad Roskilde, Dinamarca): han encontrado, mediante t¨¦cnicas de optimizaci¨®n matem¨¢tica, la ruta m¨¢s corta para visitar 2.079.471 estrellas indexadas por el proyecto Gaia de la Agencia Espacial Europea. El estudio, que puede encontrarse aqu¨ª, encuentra una ruta para visitar todas estas estrellas en... ?94.208.157,5 a?os luz! Y que adem¨¢s est¨¢ muy cerca de ser la soluci¨®n ¨®ptima. Esta aplicaci¨®n reciente e impresionante muestra la potencia matem¨¢tica de las ideas de esta disciplina.

Juanjo Ru¨¦ es profesor agregat de la Universidad Polit¨¦cnica de Catalu?a y miembro de la Barcelona Graduate School of Mathematics

Caf¨¦ y Teoremas es una secci¨®n dedicada a las matem¨¢ticas y al entorno en el que se crean, coordinado por el Instituto de Ciencias Matem¨¢ticas (ICMAT), en la que los investigadores y miembros del centro describen los ¨²ltimos avances de esta disciplina, comparten puntos de encuentro entre las matem¨¢ticas y otras expresiones sociales y culturales y recuerdan a quienes marcaron su desarrollo y supieron transformar caf¨¦ en teoremas. El nombre evoca la definici¨®n del matem¨¢tico h¨²ngaro Alfred R¨¦nyi: ¡°Un matem¨¢tico es una m¨¢quina que transforma caf¨¦ en teoremas¡±.

Edici¨®n y coordinaci¨®n: ?gata A. Tim¨®n Garc¨ªa-Longoria (ICMAT)

Puedes seguir a MATERIA en Facebook, Twitter, Instagram o suscribirte aqu¨ª a nuestra newsletter