Nanotubos y neuronas

Nuestras galletas circulares de la semana pasada, al crecer dentro del horno y comprimirse mutuamente, formar¨ªan (formaron: me sucedi¨® realmente) una red hexagonal semejante a la de un panal de abeja. De hecho, las abejas no construyen hex¨¢gonos directamente, sino que van formando celdillas circulares ¡ªcil¨ªndricas, quiero decir¡ª que al crecer y apretarse unas contra otras dan lugar a la consabida configuraci¨®n hexagonal.

Se sabe desde antiguo que un teselado hexagonal, o sea, una ret¨ªcula en forma de panal de abeja, es la forma ¨®ptima de dividir una superficie en zonas de la misma ¨¢rea y con el m¨ªnimo per¨ªmetro total; pero hasta finales del siglo pasado solo fue una conjetura (no en vano denominada la ¡°conjetura del panal de abeja¡±). La conjetura, ahora ya teorema, fue demostrada en 1999 por el matem¨¢tico estadounidense Thomas Callister Hales.

El hex¨¢gono es uno de los tres pol¨ªgonos regulares que pueden teselar el plano, junto con el cuadrado y el tri¨¢ngulo equil¨¢tero. Si form¨¢ramos una superficie plana pegando entre s¨ª, por los bordes, teselas hexagonales regulares, ?cu¨¢l ser¨ªa el ahorro en pegamento con respecto a la misma superficie formada por cuadrados iguales, tambi¨¦n pegados entre s¨ª poniendo pegamento en todos sus bordes y en toda la longitud de los mismos? (Se considera una gran superficie que permite despreciar el hecho de que el per¨ªmetro de un ¨¢rea teselada con hex¨¢gonos es una l¨ªnea quebrada).

Nanotubos de carbono

Un nanotubo es una estructura qu¨ªmica cil¨ªndrica cuyo di¨¢metro es del orden de los nan¨®metros (recordemos que un nan¨®metro es la millon¨¦sima parte de un mil¨ªmetro). Aunque los hay de otros materiales, los nanotubos por excelencia, como ve¨ªamos la semana pasada, son los de carbono, que vienen a ser como diminutas l¨¢minas de grafito de un solo ¨¢tomo de grosor (o lo que es lo mismo, de grafeno) enrolladas y con los bordes unidos para formar un cilindro muy alargado, una especie de microcapilar de unas micras de longitud y un di¨¢metro nanom¨¦trico. Por sus extraordinarias propiedades mec¨¢nicas, el¨¦ctricas y t¨¦rmicas, las aplicaciones de los nanotubos son muchas y muy prometedoras, sobre todo en la miniaturizaci¨®n de componentes electr¨®nicos, por lo que desempe?ar¨¢n un papel fundamental en el futuro desarrollo de la inform¨¢tica.

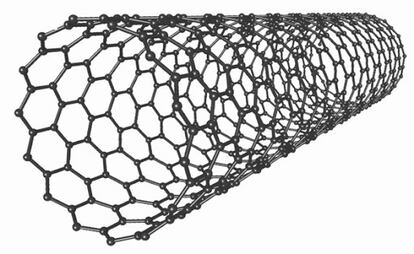
Los nanotubos pueden ser de pared simple (SWNT: Single-Walled NanoTube) o de pared m¨²ltiple (MWNT: Multi-Walled NanoTube). Los segundos pueden estar formados por varios tubos conc¨¦ntricos, o bien por una l¨¢mina multicapa de grafito enrollada como un pergamino.

Tal vez las aplicaciones m¨¢s espectaculares de los nanotubos se produzcan -se est¨¢n produciendo ya- en el terreno de la neurofisiolog¨ªa. Se ha comprobado que pueden intervenir eficazmente en la formaci¨®n de sinapsis, las estructuras a trav¨¦s de las cuales las c¨¦lulas nerviosas se comunican entre s¨ª, y tambi¨¦n pueden propiciar el crecimiento de las neuronas. Esto significa que los nanotubos pueden facilitar la regeneraci¨®n neuronal y crear un nexo artificial entre grupos de neuronas cuya conexi¨®n ha quedado interrumpida. Entre otras posibilidades, esta propiedad de los nanotubos de carbono -y tambi¨¦n de otros materiales- abre un nuevo y esperanzador camino para el tratamiento de personas con da?os en la m¨¦dula espinal.

Y hablando de nanotubos y neuronas, cabe se?alar que a finales del siglo pasado Roger Penrose (reciente premio Nobel de f¨ªsica por sus trabajos sobre los agujeros negros) y Stuart Hameroff sugirieron que la red de microt¨²bulos de las neuronas podr¨ªa funcionar como un computador cu¨¢ntico responsable de nuestra consciencia. La idea ha sido ampliamente debatida y en varias ocasiones refutada, pero abre una interesante v¨ªa de investigaci¨®n.

Carlo Frabetti es escritor y matem¨¢tico, miembro de la Academia de Ciencias de Nueva York. Ha publicado m¨¢s de 50 obras de divulgaci¨®n cient¨ªfica para adultos, ni?os y j¨®venes, entre ellos ¡®Maldita f¨ªsica¡¯, ¡®Malditas matem¨¢ticas¡¯ o ¡®El gran juego¡¯. Fue guionista de ¡®La bola de cristal¡¯.

Puedes seguir a MATERIA en Facebook, Twitter, Instagram o suscribirte aqu¨ª a nuestra newsletter