?Cu¨¢nto se puede anudar una cuerda sobre s¨ª misma?
El n¨²mero de cruces de los nudos permite clasificarlos matem¨¢ticamente

En matem¨¢ticas muchas veces partimos de una pregunta sencilla, que nos lleva por caminos insospechados. Por ejemplo, ?cu¨¢ntas veces es posible anudar una cuerda sobre s¨ª misma? En el mundo real, diversos impedimentos f¨ªsicos determinan la respuesta: la longitud de la cuerda, su capacidad el¨¢stica y grosor¡ Si despojamos a la pregunta de todas estas restricciones f¨ªsicas nos quedamos con una pregunta matem¨¢tica.
Un nudo matem¨¢tico es una curva el¨¢stica que se enreda en el espacio y que se puede deformar, manipulando sus partes sin romperlas. Los nudos matem¨¢ticos tienen pegados sus extremos, como la l¨ªnea que dibuja un c¨ªrculo. Ese es el nudo m¨¢s sencillo, el nudo trivial; pero no es el ¨²nico.
La diversidad de estos objetos matem¨¢ticos es infinita y una de las labores de la teor¨ªa de los nudos -que es un ¨¢rea de la topolog¨ªa-, es describirla. Para ello, hay que determinar cu¨¢ndo dos nudos son el mismo: lo ser¨¢n cuando es posible deformar uno en el otro, sin romperlo. Con suerte, este proceso termina en alg¨²n momento, cuando son iguales, pero, por el contrario, si no lo son, podemos invertir much¨ªsimo tiempo sin llegar a ninguna conclusi¨®n.
Para ahorrarnos este camino, la teor¨ªa de los nudos se encarga de identificar propiedades matem¨¢ticas que se pueden comprobar m¨¢s f¨¢cilmente. De estas, la m¨¢s sencilla es contar cuantas veces se cruza la curva al dibujarla en una hoja de papel, indicando qu¨¦ parte cruza por arriba y qu¨¦ parte por debajo, en cada cruce.
Sin embargo, un mismo nudo puede tener much¨ªsimos diagramas diferentes; no solo de acuerdo al punto de vista desde el que se dibuje, sino que, adem¨¢s, podr¨ªa haber algunos cruces que desaparecer¨ªan simplemente torciendo, un poco, alguna parte del nudo.
La cantidad m¨ªnima de cruces que se pueden conseguir en un diagrama del nudo permite decir si dos nudos son diferentes; por ejemplo, si uno tiene tres y el otro cuatro. Y tambi¨¦n permite organizar los nudos en un gran cat¨¢logo, empezando por el m¨¢s simple: el c¨ªrculo, o nudo trivial, que se puede dibujar sin ning¨²n cruce.
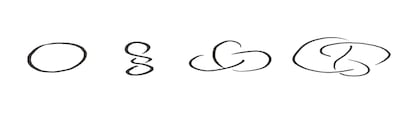
Todos los nudos que se pueden dibujar con uno o dos cruces se pueden manipular de tal manera que queden id¨¦nticos a una circunferencia. Solo hay un nudo con tres cruces y se le conoce como el ¡°nudo tr¨¦bol¡±. El ¡°nudo ocho¡± es el ¨²nico que se puede dibujar con cuatro cruces, pero a partir de ah¨ª, la diversidad crece r¨¢pidamente. El cat¨¢logo de nudos con hasta diez cruces tiene 250 nudos diferentes, y con hasta 19 la cantidad asciende a m¨¢s de 300 millones.
Un nudo salvaje tiene una cantidad infinita de cruces y da respuesta a la pregunta con la que empez¨¢bamos este texto. Para imaginarlo, podemos valernos de una receta que, aunque infinita, es relativamente simple. Un ingrediente importante de la receta son los espejos esf¨¦ricos, que muestran, en su superficie, la imagen reflejada de todo el espacio, como si estuviera en el interior de la esfera. Este espejo deforma la mayor¨ªa de las figuras: las l¨ªneas rectas se observan curvas y es inevitable pensar en un pez al mirar nuestro rostro reflejado. La ¨²nica figura que no cambia al reflejarse, salvo por su tama?o, es la figura de cualquier otra esfera.
La clave de la receta est¨¢ en esta propiedad, pues, esa otra esfera tambi¨¦n podr¨ªa estar hecha de espejo y, en ese caso, si nos fijamos con cuidado, podr¨ªamos observar, en el reflejo de esa esfera, la imagen reflejada de la esfera inicial¡ un trabalenguas. Para construir un nudo salvaje se parte de un nudo de los del cat¨¢logo, cualquiera sirve salvo el nudo trivial, y se necesitan tambi¨¦n algunos cuantos espejos esf¨¦ricos, que pueden ser de diferentes tama?os. Entonces, se engarzan las esferas, una a una, en una cuerda imaginaria, procurando que est¨¦n suficientemente apretadas para que las esferas consecutivas se toquen en un punto, para formar un collar.
A continuaci¨®n, se anuda el collar de acuerdo al diagrama del nudo elegido y se cierra por sus extremos, procurando que las esferas de las puntas tambi¨¦n se toquen. En cada una de las esferas del collar se refleja una copia del resto del collar y estos pedazos de collar se conectan, en esferas consecutivas, formando un nuevo collar, hecho de esferas m¨¢s peque?as. Este nuevo collar es m¨¢s intrincado que el anterior, pues en cada pedazo se puede ver la forma del nudo repetido en cada esfera. Adem¨¢s, como tambi¨¦n est¨¢ hecho de esferas reflejantes podemos repetir el paso anterior en este nuevo collar y as¨ª otra vez, y otra vez¡ hasta el infinito.
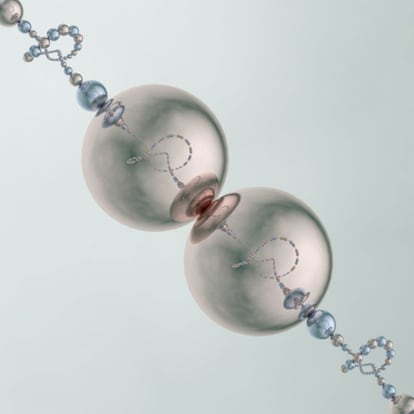
El nudo salvaje tiene infinitos detalles cada vez m¨¢s peque?os. Y, gracias a las matem¨¢ticas, sabemos que dentro de todos estos collares solo cabe una delgada curva sin extremos, infinitamente anudada: un nudo salvaje. Efectivamente, en cada paso, las esferas reducen su tama?o; y en cada paso agregamos m¨¢s y m¨¢s cruces.
Si bien hay f¨®rmulas expl¨ªcitas y precisas que describen exactamente la posici¨®n de las esferas reflejadas en el interior, a diferencia de los espejos, que nos muestran una imagen plana en la superficie, esta idea nos permite imaginarnos (y estudiar, desde el punto de vista de las matem¨¢ticas) los nudos salvajes.
Aubin Arroyo es investigador en el Instituto de Matem¨¢ticas de la Universidad Nacional Aut¨®noma de M¨¦xico (UNAM)
Caf¨¦ y Teoremas es una secci¨®n dedicada a las matem¨¢ticas y al entorno en el que se crean, coordinado por el Instituto de Ciencias Matem¨¢ticas (ICMAT), en la que los investigadores y miembros del centro describen los ¨²ltimos avances de esta disciplina, comparten puntos de encuentro entre las matem¨¢ticas y otras expresiones sociales y culturales y recuerdan a quienes marcaron su desarrollo y supieron transformar caf¨¦ en teoremas. El nombre evoca la definici¨®n del matem¨¢tico h¨²ngaro Alfred R¨¦nyi: ¡°Un matem¨¢tico es una m¨¢quina que transforma caf¨¦ en teoremas¡±.
Edici¨®n y coordinaci¨®n: ?gata A. Tim¨®n G Longoria (ICMAT).
Puedes seguir a MATERIA en Facebook, Twitter e Instagram, o apuntarte aqu¨ª para recibir nuestra newsletter semanal.
Tu suscripci¨®n se est¨¢ usando en otro dispositivo
?Quieres a?adir otro usuario a tu suscripci¨®n?
Si contin¨²as leyendo en este dispositivo, no se podr¨¢ leer en el otro.
FlechaTu suscripci¨®n se est¨¢ usando en otro dispositivo y solo puedes acceder a EL PA?S desde un dispositivo a la vez.
Si quieres compartir tu cuenta, cambia tu suscripci¨®n a la modalidad Premium, as¨ª podr¨¢s a?adir otro usuario. Cada uno acceder¨¢ con su propia cuenta de email, lo que os permitir¨¢ personalizar vuestra experiencia en EL PA?S.
?Tienes una suscripci¨®n de empresa? Accede aqu¨ª para contratar m¨¢s cuentas.
En el caso de no saber qui¨¦n est¨¢ usando tu cuenta, te recomendamos cambiar tu contrase?a aqu¨ª.
Si decides continuar compartiendo tu cuenta, este mensaje se mostrar¨¢ en tu dispositivo y en el de la otra persona que est¨¢ usando tu cuenta de forma indefinida, afectando a tu experiencia de lectura. Puedes consultar aqu¨ª los t¨¦rminos y condiciones de la suscripci¨®n digital.
M¨¢s informaci¨®n


































































