Adi¨®s a un matem¨¢tico surrealista y m¨¢gico

La pandemia del coronavirus no respeta ni a los dioses del olimpo matem¨¢tico. El pasado 11 de abril falleci¨® el gran matem¨¢tico brit¨¢nico John Horton Conway (Liverpool, 1937), en Nueva Jersey, Estados Unidos. Su colega, medalla Fields y premio Abel, sir Michael Atiyah, le describi¨® como ¡°el matem¨¢tico m¨¢s m¨¢gico del mundo¡±. Muchas de sus grandes contribuciones cient¨ªficas nacieron de su gran afici¨®n a los juegos.

Mientras que era profesor en Cambridge, entre 1969 a 1970, vivi¨® su gran periodo de inspiraci¨®n, similar al que experimentaron antes otros grandes cient¨ªficos como Einstein y Newton. Hizo descubrimientos que llegaron m¨¢s all¨¢ de la comunidad cient¨ªfica, entre los que destaca el famoso juego de la vida. Es un sencillo juego para una persona, que reproduce interesantes analog¨ªas con el crecimiento, alternancia y fallecimiento de sociedades de organismos vivos. De esta manera, se considera un juego de simulaci¨®n, ya que imita el comportamiento de procesos de la naturaleza. Sin embargo, para Conway la motivaci¨®n de desentra?ar el juego era puramente matem¨¢tica: quer¨ªa encontrar un sistema universal, capaz de realizar c¨¢lculos arbitrarios, si se dispusiese de suficiente tiempo y suficiente memoria, es decir, una especie de ordenador infinitamente programable

Empleaba un tablero (infinito) dividido en cuadrados, como el del conocido juego del Go. Cada posici¨®n tiene ocho celdas vecinas: cuatro con lados adyacentes y cuatro en la diagonal con un v¨¦rtice en com¨²n. Cada organismo vivo queda representado por una ficha en una celdilla, y el juego consiste en observar su evoluci¨®n a lo largo del tiempo, aplicando unas sencillas reglas que determinan los nacimientos, muertes y supervivientes tras cada jugada:

¡¤ Supervivientes. Cada ficha con dos o tres vecinos vivos sobrevive al siguiente turno.

¡¤ Muertes. Cada ficha rodeada por cuatro o m¨¢s vecinos muere por superpoblaci¨®n. Pero tambi¨¦n las fichas que tengan solo uno o ning¨²n vecino vivo mueren por aislamiento

¡¤ Nacimientos. Cada celda vac¨ªa que tenga exactamente tres vecinos ¨Cni m¨¢s ni menos- se convierte en una celda de nacimiento. En la siguiente generaci¨®n, en esa celda vac¨ªa aparece una nueva ficha.

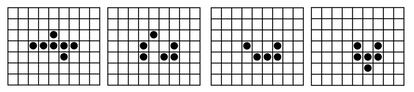
A partir de configuraciones iniciales y reglas muy sencillas surgen patrones extremadamente complicados. Aunque el juego de la vida es completamente determinista no podemos predecir completamente c¨®mo se desarrollar¨¢n estas configuraciones a largo plazo, por ejemplo, no podr¨ªamos garantizar que vayan a adoptar una configuraci¨®n predeterminada tras una serie de pasos del juego. Llevando esta analog¨ªa al comportamiento humano, podr¨ªamos pensar que aunque ¨¦ste pueda tener un origen determinista simple, no implica que el comportamiento resultante sea siempre predecible.

El juego de la vida de Conway es un ejemplo de aut¨®mata celular, es decir, un sistema din¨¢mico que evoluciona en un n¨²mero de pasos. El primero en idear un sistema de este tipo fue John von Neumann, cuya c¨¢tedra ocup¨® Conway en la Universidad de Princeton en 1986. Los aut¨®matas celulares se han aplicado en ciencia de la computaci¨®n, f¨ªsica matem¨¢tica, sistemas complejos, biolog¨ªa, ingenier¨ªa¡­ Por ejemplo, est¨¢n en la base de la computaci¨®n en paralelo y en el dise?o de ordenadores cuya arquitectura est¨¦ basada en principios y materiales biolo?gicos.

El juego de la vida de Conway es un ejemplo de aut¨®mata celular, es decir, un sistema din¨¢mico que evoluciona en un n¨²mero de pasos

Tambi¨¦n pensando en el juego del Go, invent¨® un nuevo tipo de n¨²meros, los ¡°n¨²meros surreales¡±. En el juego chino, en la estructura de los finales de las partidas se forman diferentes subjuegos, al separarse las fichas restantes en el tablero. Conway observ¨® c¨®mo se pod¨ªan sumar estos subjuegos y a partir de esta idea describi¨® una nueva clase de n¨²meros, los n¨²meros surreales, en los que cada n¨²mero se define a partir de los anteriores. Adem¨¢s de los n¨²meros reales, los n¨²meros surreales contienen n¨²meros infinitesimales, es decir, n¨²meros infinitamente peque?os, y otras familias de n¨²meros infinitos.

Otro de los descubrimientos de Conway durante su annus mirabilis fue el grupo de Conway, que surge al buscar la mejor forma de apilar esferas en dimensi¨®n 24, de forma que cada esfera est¨¢ en contacto con otras 196.560 esferas, lo que supone la configuraci¨®n ¡°m¨¢s densa¡± para esta dimensi¨®n.

Ser¨ªa imposible seguir detallando todos los campos en los que destac¨® Conway: ¨¢lgebra, teor¨ªa de n¨²meros, teor¨ªa de nudos, combinatoria, probabilidad, an¨¢lisis¡­ Incluso en mec¨¢nica cu¨¢ntica prob¨®, junto a Simon B. Kochen en 2006, el famoso y sorprendente Teorema del libre albedr¨ªo (Will Free Theorem) que afirma, a grandes rasgos, que al igual que los humanos tenemos libre albedr¨ªo, tambi¨¦n lo tienen las part¨ªculas elementales, bajo ciertas hip¨®tesis.

Asistir a las charlas de Conway era una experiencia maravillosa, casi m¨¢gica. En Princeton prefer¨ªa dar las clases de primer curso, las que normalmente nadie quiere dar, porque son demasiado b¨¢sicas, para persuadir a los estudiantes en convertirse en futuros matem¨¢ticos. En los veranos, participaba frecuentemente en campamentos de matem¨¢ticas para motivar a las generaciones venideras. All¨ª se presentaba solamente con una baraja, unas monedas, cuerdas, unos dados y otros utensilios inveros¨ªmiles y con ellos era capaz de improvisar y desarrollar ideas matem¨¢ticas cautivando a la audiencia.

La vida de Conway fue intensa, con momentos maravillosos y otros muy dif¨ªciles, incluido un intento de suicidio, pero lo que siempre perdurar¨¢ es su m¨¢gico legado.

David Mart¨ªn de Diego es investigador cient¨ªfico del CSIC en el ICMAT y vicepresidente de la Real Sociedad Matem¨¢tica Espa?ola

Caf¨¦ y Teoremas es una secci¨®n dedicada a las matem¨¢ticas y al entorno en el que se crean, coordinado por el Instituto de Ciencias Matem¨¢ticas (Icmat), en la que los investigadores y miembros del centro describen los ¨²ltimos avances de esta disciplina, comparten puntos de encuentro entre las matem¨¢ticas y otras expresiones sociales y culturales y recuerdan a quienes marcaron su desarrollo y supieron transformar caf¨¦ en teoremas. El nombre evoca la definici¨®n del matem¨¢tico h¨²ngaro Alfred R¨¦nyi: ¡°Un matem¨¢tico es una m¨¢quina que transforma caf¨¦ en teoremas¡±.

Edici¨®n y coordinaci¨®n: ?gata Tim¨®n (Icmat).

Puedes seguir a Materia en Facebook, Twitter, Instagram o suscribirte aqu¨ª a nuestra newsletter.