Del cuadrado m¨¢gico al sudoku

Puesto que se puede formar un cuadrado m¨¢gico de orden n con los n² primeros n¨²meros naturales, tambi¨¦n se podr¨¢ formar con cualesquiera n² n¨²meros consecutivos, puesto que si le sumamos un mismo n¨²mero x a todos los de un cuadrado m¨¢gico, el cuadrado seguir¨¢ siendo m¨¢gico (con la constante aumentada en nx).

Con los nueve primeros n¨²meros impares se puede formar un cuadrado m¨¢gico de constante m¨¢gica 27: 15, 1, 11; 5, 9, 13; 7, 17, 3 (las comas separan los n¨²meros de una misma fila, y los puntos y coma separan una fila de otra).

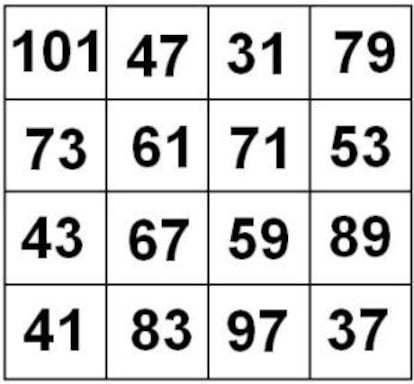
Se pueden formar cuadrados m¨¢gicos con n¨²meros primos, aunque no es f¨¢cil hallarlos. Un ejemplo se puede ver en la imagen de la derecha:

En este caso, el m¨¢s dif¨ªcil todav¨ªa ser¨ªa formar un cuadrado m¨¢gico con n¨²meros primos consecutivos; de momento, me limitar¨¦ a decir que es posible.

Los cuadrados m¨¢gicos est¨¢n estrechamente emparentados con los cuadrados latinos, en los que n n¨²meros (u otros signos) se repiten en una cuadr¨ªcula de nxn de forma que cada n¨²mero aparezca una y solo una vez en cada fila y cada columna. Se llaman cuadrados latinos porque Leonhard Euler los estudi¨® utilizando caracteres latinos en lugar de n¨²meros (aunque no fue ¨¦l quien los invent¨®: los primeros ejemplos conocidos se remontan a un manuscrito ¨¢rabe del siglo XIII).

Obs¨¦rvese que el popular sudoku (una vez resuelto correctamente) es un cuadrado latino de 9x9, con la condici¨®n adicional de que en cada subcuadr¨ªcula de 3x3 tambi¨¦n tienen que estar los d¨ªgitos del 1 al 9 una y solo una vez.

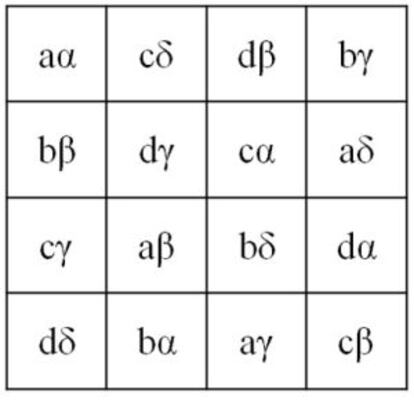
Una variante especialmente interesante, y con numerosas aplicaciones, es la de los cuadrados grecolatinos. Un cuadrado grecolatino de orden n es una cuadr¨ªcula de nxn en la cual hay en cada casilla un par ordenado de los n¨²meros 1, 2, 3¡­ n (u otros signos), de forma que los dos cuadrados formados solo por los primeros t¨¦rminos de cada par y solo por los segundos sean cuadrados latinos, y cada una de las n² posibles parejas de n¨²meros aparezcan una y solo una vez en la cuadr¨ªcula. Se llaman as¨ª porque Euler los estudi¨® utilizando, en vez de n¨²meros, caracteres latinos para los primeros t¨¦rminos y griegos para los segundos, como en el ejemplo de la izquierda.

Y ahora, aunque no parezca venir muy a cuento, un toque de poes¨ªa. La sextina es una curiosa composici¨®n po¨¦tica en la que se parte de una estrofa de seis versos endecas¨ªlabos que no riman entre s¨ª, y las seis palabras finales de los versos se repiten en otras cinco estrofas de seis versos, pero siempre ocupando lugares distintos: en la segunda estrofa, la terminaci¨®n del ¨²ltimo verso de la primera estrofa pasa al primer lugar, con lo que la primera terminaci¨®n se convierte en la segunda; la pen¨²ltima pasa al tercer lugar, con lo que la segunda se convierte en la cuarta; la antepen¨²ltima pasa al quinto lugar y la tercera se convierte en la sexta. Veamos, a modo de ejemplo, las dos primeras estrofas de Apolog¨ªa y petici¨®n, una famosa sextina de Jaime Gil de Biedma:

?Y qu¨¦ decir de nuestra madre Espa?a,

este pa¨ªs de todos los demonios

en donde el mal gobierno, la pobreza

no son, sin m¨¢s, pobreza y mal gobierno

sino un estado m¨ªstico del hombre,

la absoluci¨®n final de nuestra historia?

De todas las historias de la Historia

sin duda la m¨¢s triste es la de Espa?a,

porque termina mal. Como si el hombre,

harto ya de luchar con sus demonios,

decidiese encargarles el gobierno

y la administraci¨®n de su pobreza.

Para determinar el orden de las terminaciones en la tercera estrofa, hacemos con la segunda lo mismo que hemos hecho con la primera, y as¨ª sucesivamente¡­

?Tiene alg¨²n sentido hablar de las sextinas en este contexto?

?Se pueden colocar los reyes, caballos, sotas y ases de una baraja formando un cuadrado de 4x4 tal que cada fila y cada columna contenga todas las figuras y todos los palos? Y si lo conseguimos, ?qu¨¦ habremos construido?

Adem¨¢s de constituir un llamativo dise?o para un edred¨®n, ?qu¨¦ representa la colorista ilustraci¨®n de portada?

Carlo Frabetti

Escritor y matem¨¢tico, miembro de la Academia de Ciencias de Nueva York, ha publicado m¨¢s de 50 obras de divulgaci¨®n cient¨ªfica para adultos, ni?os y j¨®venes, entre ellos ¡®Maldita f¨ªsica¡¯, ¡®Malditas matem¨¢ticas¡¯ o ¡®El gran juego¡¯. Fue guionista de ¡®La bola de cristal¡¯