Al pasar la barca

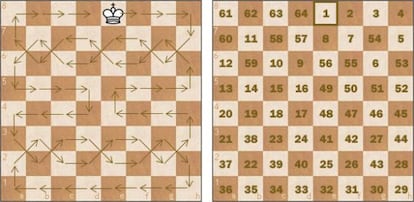
En el acertijo anterior, al dar siete n¨²meros de una fila de un cuadrado m¨¢gico de orden 8, en realidad los damos todos, pues su suma tiene que ser la constante m¨¢gica del cuadrado; puesto que en el cuadrado est¨¢n los n¨²meros del 1 al 64, la suma total ser¨¢ 2.080, y como las ocho filas tienen que sumar lo mismo, la constante es 2.080 : 8 = 260. Por lo tanto, el octavo n¨²mero de la primera fila es 260 ¨C 61 ¨C 62 ¨C 63 ¨C 64 ¨C 1 ¨C 2 ¨C 3 = 4, y el de la octava fila es 260 ¨C 36 ¨C 35 ¨C 34 ¨C 33 ¨C 32 ¨C 31 ¨C 30 = 29. A pesar de tener dos filas completas, no es f¨¢cil hallar la soluci¨®n que vemos en la figura (obs¨¦rvese la elegante simetr¨ªa del recorrido del rey, a la izquierda).

Pero ya est¨¢ bien (por el momento) de recorridos individuales: un fil¨®sofo que va a visitar a un amigo, un paseante que cruza puentes, un ciclista que va y vuelve de la playa, un punto que recorre las aristas de un poliedro¡­ Veamos ahora algunos interesantes recorridos que implican a varias personas, animales o cosas, como los que aparecen en un tema cl¨¢sico de los acertijos l¨®gicos: el de la barca con la que hay que cruzar un r¨ªo cumpliendo ciertos requisitos.

Uno de los m¨¢s sencillos y conocidos, pero no por ello desde?able, es el del pastor que va con un lobo, una cabra y una enorme col y tiene que cruzar un r¨ªo en una peque?a barca que solo le permite llevar una cosa a la vez, con el agravante de que no puede dejar solos al lobo y a la cabra (pues el primero se comer¨ªa a la segunda) ni la col con la cabra (pues el artiod¨¢ctilo se comer¨ªa la hortaliza).

Otro muy similar es el de la familia gordita: el padre y la madre pesan cien kilos cada uno, y el hijo y la hija cincuenta por cabeza, y tienen que cruzar un r¨ªo en una barca que solo puede llevar como m¨¢ximo cien kilos.

?C¨®mo pueden cruzar el r¨ªo de forma que nunca una mujer quede en compa?¨ªa de otro hombre si su marido no est¨¢ presente?

Y un tercer cl¨¢sico: tres misioneros y tres can¨ªbales llegan a un r¨ªo y quieren pasar a la otra orilla. Disponen de una barca en la que solo pueden viajar dos personas, y en ning¨²n momento puede haber m¨¢s can¨ªbales que misioneros en una orilla, porque los primeros se comer¨ªan a los segundos.

?C¨®mo pueden pasar todos al otro lado del r¨ªo?

Y una variante del anterior: tres maridos celosos y sus respectivas esposas tienen que cruzar un r¨ªo en una barca que solo puede llevar a dos personas en cada viaje. ?C¨®mo pueden cruzar el r¨ªo de forma que nunca una mujer quede en compa?¨ªa de otro hombre si su marido no est¨¢ presente?

Y sin salir del tema de las barcas y los r¨ªos, pero enfocado desde otro ¨¢ngulo, he aqu¨ª un acertijo propuesto por un lector, Jos¨¦ Hinojosa, en una de las primeras entregas de esta secci¨®n (ver ¨²ltima entrada de la 9? p¨¢gina de comentarios de Un fil¨®sofo de ida y vuelta):

Dos barcas parten simult¨¢neamente de las orillas opuestas y paralelas de un r¨ªo. Al cabo de cierto tiempo se cruzan a 200 metros de la orilla derecha. Contin¨²an su viaje y al llegar a la orilla opuesta cada barca permanece parada 10 minutos, tras lo cual vuelven a salir en sentidos opuestos, cruz¨¢ndose otra vez, a 100 metros de la orilla izquierda. ?Qu¨¦ anchura tiene el r¨ªo?

Invito a nuestras lectoras y lectores a proponer otros acertijos sobre el inagotable tema de las barcas y los r¨ªos.

Carlo Frabetti

Escritor y matem¨¢tico, miembro de la Academia de Ciencias de Nueva York, ha publicado m¨¢s de 50 obras de divulgaci¨®n cient¨ªfica para adultos, ni?os y j¨®venes, entre ellos ¡®Maldita f¨ªsica¡¯, ¡®Malditas matem¨¢ticas¡¯ o ¡®El gran juego¡¯. Fue guionista de ¡®La bola de cristal¡¯