El acertijo de los posavasos
Una adivinanza supuestamente aparecida en un posavasos de un bar y una indigesti¨®n de pastelillos navide?os. Buen provecho.
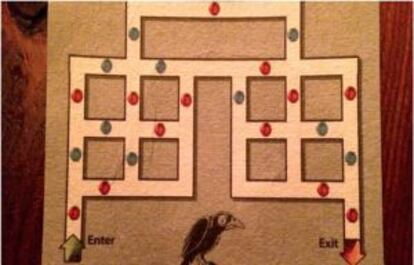
La semana pasada se ped¨ªa hallar el punto de un tri¨¢ngulo cuya suma de distancias a los v¨¦rtices es m¨ªnima; pues bien, ese punto se conoce como punto de Fermat, o de Fermat-Torricelli (pues parece ser que Fermat le plante¨® el problema a su colega Torricelli y este lo resolvi¨®), y se puede hallar mediante la construcci¨®n de la figura.
Sobre cada lado del tri¨¢ngulo, ABC, construimos un tri¨¢ngulo equil¨¢tero, y luego unimos los v¨¦rtices de ABC con los respectivos v¨¦rtices exteriores de los tri¨¢ngulos opuestos; el punto de intersecci¨®n de los segmentos as¨ª obtenidos es el punto de Fermat (dejo la demostraci¨®n en manos de mis sagaces lectoras y lectores).
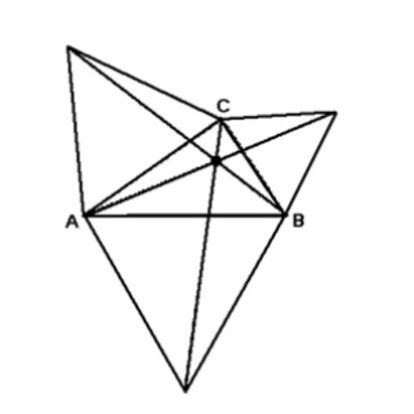
Hay una elegante demostraci¨®n gr¨¢fica de que las tres alturas de un tri¨¢ngulo se cortan en un punto (llamado ortocentro). Trazamos por cada v¨¦rtice del tri¨¢ngulo una paralela al lado opuesto, y de este modo obtenemos otro tri¨¢ngulo cuyas mediatrices son las alturas del primero; y las mediatrices de un tri¨¢ngulo se cortan en el punto que equidista de los tres v¨¦rtices. Esto ¨²ltimo es f¨¢cil de demostrar: por definici¨®n, todos los puntos de la mediatriz del lado A¡¯B¡¯ equidistan de los v¨¦rtices A¡¯ y B¡¯, y todos los puntos de la mediatriz del lado A¡¯C¡¯ equidistan de los v¨¦rtices A¡¯ y C¡¯; por lo tanto, el punto de intersecci¨®n de ambas mediatrices equidista de B¡¯ y C¡¯, luego tambi¨¦n pertenece a la mediatriz del lado B¡¯C¡¯.
En cuanto al tri¨¢ngulo amoroso, si llamamos A, B y C a los tres jugadores de acuerdo con sus iniciales, la pelota solo puede recorrer dos circuitos: ABC y AC. Como ambos circuitos son igualmente probables, de cada cinco pases (ABC + AC) la pelota ir¨¢ dos veces a A, dos veces a C y una a B. Las probabilidades respectivas son, por tanto, 2/5, 2/5 y 1/5.
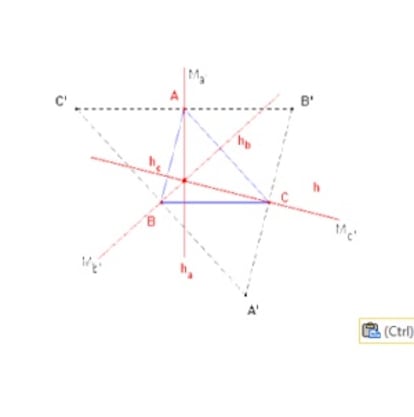
Posavasos y pastelillos
Este acertijo (v¨¦ase la imagen que encabeza la noticia, arriba a la izquierda), supuestamente aparecido en un posavasos de un bar, ha arrasado en las redes sociales en los ¨²ltimos d¨ªas: se trata de entrar por la izquierda en el circuito de la figura y salir por la derecha, pasando alternativamente por puntos de distinto color, o sea, seg¨²n la secuencia rojo-azul-rojo-azul-rojo¡
Y para empezar el a?o con buen pie, otro recorrido peculiar, esta vez un cl¨¢sico navide?o del gran Henry Dudeney, maestro de inventores de acertijos. Seg¨²n una vieja tradici¨®n, tendr¨¢s tantos d¨ªas de suerte al a?o siguiente como pastelillos de ciruela comas en Navidad, de modo que aqu¨ª tienes la ocasi¨®n de conseguir un buen n¨²mero de ellos.

No es dif¨ªcil recorrer los 64 pastelillos de la figura sin pasar dos veces por ninguno de ellos, pero la cosa se complica si hay que empezar por el pastelillo de la parte superior marcado con una ramita de acebo y hay que efectuar 21 trazos rectos, el ¨²ltimo de los cuales ha de terminar en el otro pastelillo marcado con la ramita de acebo en la parte inferior y, adem¨¢s, antes hay que llegar al pastelillo humeante de la ¨²ltima fila al final del d¨¦cimo trazo. Buen provecho.
Carlo Frabetti
Escritor y matem¨¢tico, miembro de la Academia de Ciencias de Nueva York, ha publicado m¨¢s de 50 obras de divulgaci¨®n cient¨ªfica para adultos, ni?os y j¨®venes, entre ellos ¡®Maldita f¨ªsica¡¯, ¡®Malditas matem¨¢ticas¡¯ o ¡®El gran juego¡¯. Fue guionista de ¡®La bola de cristal¡¯
Tu suscripci¨®n se est¨¢ usando en otro dispositivo
?Quieres a?adir otro usuario a tu suscripci¨®n?
Si contin¨²as leyendo en este dispositivo, no se podr¨¢ leer en el otro.
FlechaTu suscripci¨®n se est¨¢ usando en otro dispositivo y solo puedes acceder a EL PA?S desde un dispositivo a la vez.
Si quieres compartir tu cuenta, cambia tu suscripci¨®n a la modalidad Premium, as¨ª podr¨¢s a?adir otro usuario. Cada uno acceder¨¢ con su propia cuenta de email, lo que os permitir¨¢ personalizar vuestra experiencia en EL PA?S.
?Tienes una suscripci¨®n de empresa? Accede aqu¨ª para contratar m¨¢s cuentas.
En el caso de no saber qui¨¦n est¨¢ usando tu cuenta, te recomendamos cambiar tu contrase?a aqu¨ª.
Si decides continuar compartiendo tu cuenta, este mensaje se mostrar¨¢ en tu dispositivo y en el de la otra persona que est¨¢ usando tu cuenta de forma indefinida, afectando a tu experiencia de lectura. Puedes consultar aqu¨ª los t¨¦rminos y condiciones de la suscripci¨®n digital.
Sobre la firma


































































