Buscarle tres pies al gato
Algunos acertijos tienen una soluci¨®n clara y aparentemente ¨²nica; pero si le buscamos tres pies al gato (como suelen hacer muchos lectores) podemos llevarnos algunas sorpresas

Nos pregunt¨¢bamos la semana pasada cu¨¢ntos cortes ser¨ªan necesarios, como m¨ªnimo, para dividir un cubo en 27 cubitos. Para comprender que no se puede conseguir en menos de seis cortes, basta con darse cuenta de que cada una de las seis caras del cubito central necesita un corte distinto. Por cierto, para dividir un cubo en 64 cubitos tambi¨¦n es suficiente con seis cortes (aunque en este caso hay que reagrupar los trozos despu¨¦s de cada corte: ver detalles en la secci¨®n de comentarios). ?Hay alguna f¨®rmula general o algoritmo que permita saber cu¨¢ntos cortes ser¨¢n necesarios para dividir un cubo en n3 cubitos?
El problema del ni?o y los caramelos se resuelve mejor pasando hacia atr¨¢s la pel¨ªcula de sus encuentros e imaginando que cada amigo con el que se encuentra le da un caramelo y luego duplica los que tiene, con lo que la secuencia es: (0 + 1) x 2 = 2, (2 + 1) x 2 = 6, (6 + 1) x 2 = 14, (14 + 1) x 2 = 30, (30 + 1) x 2 = 62, (62 + 1) x 2 = 126. El ni?o sali¨® de casa con 126 caramelos.
El problema de los seis n¨²meros naturales comprendidos entre los diez primeros tiene varias soluciones (m¨¢s de las que yo cre¨ªa, debo admitirlo): 1, 6, 8 / 2, 4, 9; 4, 8, 9 / 5, 6, 10; 2, 7, 9 / 3, 5, 10; 3, 7, 8 / 4, 5, 9; 2, 6, 7 / 3, 4, 8; 1, 5, 6 / 2, 3, 7; 1, 6, 9 / 3, 3, 10; 2, 5, 10 / 1, 8, 8.
Puntos gordos y sucesiones que se bifurcan
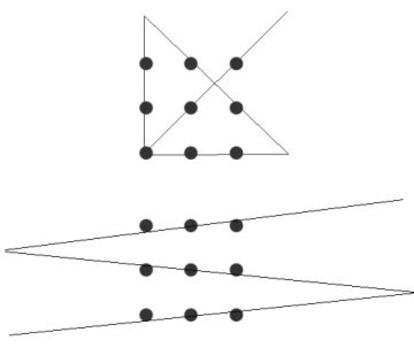
En el conocido acertijo de los nueve puntos (ver Pensar a contracorriente, 15 1 2016), podemos buscarle tres pies al gato considerando que los puntos no son inextensos, en cuyo caso admite, como vimos, la segunda soluci¨®n de la figura.
Y en el problema de la balanza desequilibrada de hace un par de semanas, si no despreciamos el peso de los brazos o consideramos que los platillos podr¨ªan no pesar lo mismo, hay infinitas soluciones.
Las sucesiones num¨¦ricas en las que, dados cinco o seis t¨¦rminos, hay que hallar los siguientes, son un cl¨¢sico de los test de inteligencia y los acertijos l¨®gicos; pero a menudo (mejor dicho, siempre) admiten m¨¢s de una soluci¨®n si le buscamos tres (o cuatro, o cinco¡) pies al gato algor¨ªtmico. Las siete sucesiones siguientes son bastante f¨¢ciles (aunque no todas) si nos conformamos con la soluci¨®n m¨¢s obvia; pero os invito a buscar, en cada caso, una segunda soluci¨®n. O m¨¢s.
2, 3, 6, 7, 16¡
1, 2, 2, 3, 2, 4¡
17, 33, 65, 129¡
4, 6, 9, 10, 14, 15¡
1, 8, 27, 64¡
5, 12, 20, 30, 43¡
1, 11, 21, 1211, 111221¡
Tu suscripci¨®n se est¨¢ usando en otro dispositivo
?Quieres a?adir otro usuario a tu suscripci¨®n?
Si contin¨²as leyendo en este dispositivo, no se podr¨¢ leer en el otro.
FlechaTu suscripci¨®n se est¨¢ usando en otro dispositivo y solo puedes acceder a EL PA?S desde un dispositivo a la vez.
Si quieres compartir tu cuenta, cambia tu suscripci¨®n a la modalidad Premium, as¨ª podr¨¢s a?adir otro usuario. Cada uno acceder¨¢ con su propia cuenta de email, lo que os permitir¨¢ personalizar vuestra experiencia en EL PA?S.
En el caso de no saber qui¨¦n est¨¢ usando tu cuenta, te recomendamos cambiar tu contrase?a aqu¨ª.
Si decides continuar compartiendo tu cuenta, este mensaje se mostrar¨¢ en tu dispositivo y en el de la otra persona que est¨¢ usando tu cuenta de forma indefinida, afectando a tu experiencia de lectura. Puedes consultar aqu¨ª los t¨¦rminos y condiciones de la suscripci¨®n digital.
Sobre la firma


































































