En busca de la caja perfecta

Habitualmente, los problemas interesantes a los que se enfrentan los matem¨¢ticos profesionales actualmente suelen ser cuestiones complicadas, tanto en su planteamiento como en su soluci¨®n. Pero hay muchos problemas que, a pesar de su sencillo planteamiento, han suscitado un gran inter¨¦s entre muchos miembros de la comunidad matem¨¢tica a lo largo de la historia. El que nos ocupa hoy es uno de ellos.

Vamos a hablar de cajas. Pero no de cualquier caja, sino de cajas con ciertas propiedades. Buscamos cajas como las que ahora mismo pod¨¦is tener en la mente, tipo las cajas de zapatos: cajas en las que las tres parejas de caras opuestas son rect¨¢ngulos (evidentemente, tambi¨¦n nos sirven cuadrados) iguales. Estas cajas se llaman cuboides. Pero vamos a pedirles tambi¨¦n que adem¨¢s cumplan que sus aristas tengan longitudes sencillas, ya que no queremos n¨²meros complicados. Por ello, para nuestras cajas vamos a elegir n¨²meros enteros para las longitudes de sus aristas.

Como ese tipo de cajas son sencillas de encontrar, vamos a a?adirle una condici¨®n m¨¢s: vamos a buscar cajas en las que las diagonales de sus caras tambi¨¦n sean n¨²meros enteros. Si las longitudes de las aristas son n¨²meros enteros, las longitudes de las diagonales son f¨¢cilmente calculables utilizando el teorema de Pit¨¢goras. Vosotros mismos pod¨¦is buscar una caja as¨ª: eleg¨ªs tres valores enteros positivos para las aristas y calcul¨¢is despu¨¦s los valores de las diagonales para ver si ¨¦stas tambi¨¦n son enteras positivas.

Si lo hac¨¦is, os dar¨¦is cuenta de que la cosa no es tan sencilla como cab¨ªa esperar. Lo normal es que, probando de esta forma, no hay¨¢is sido capaces de encontrar ninguna caja con las condiciones que hemos comentado. La pregunta ahora es: ?existen cajas con estas caracter¨ªsticas?

Y la respuesta a esta pregunta es afirmativa: s¨ª existen cajas en las que tanto las aristas como las diagonales de las caras tienen longitudes positivas. Vamos a llamar cuboides racionales a estas cajas cuyas aristas y diagonales de las caras son n¨²meros enteros positivos.

Seg¨²n parece, fue Nicholas Saunderson el primero que public¨® algo relacionado con estas cajas sobre 1740, dando una expresi¨®n param¨¦trica para encontrar infinitas de ellas. Saunderson ya conoc¨ªa en aquella ¨¦poca el siguiente resultado:

¡°Si tres n¨²meros enteros positivos (a,b,c) cumplen el?teorema de Pit¨¢goras (es decir, cumplen que a²+b²=c²), entonces los n¨²meros (x,y,z) calculados de esta forma

x=4abc, y=a(4b²-c²), z=b(4a²-c²)

son las aristas de un cuboide racional.¡±

Es decir, (x,y,z) son las aristas de una caja como las que estamos buscando.

Como hemos dicho, esto aparece en una publicaci¨®n a nombre de Saunderson sobre 1740, pero actualmente a este tipo de cajas se las conoce como cajas de Euler (en ingl¨¦s se las suele llamar Euler brick). Es cierto que Euler tambi¨¦n las estudi¨®, y que encontr¨® algunas propiedades interesantes sobre ellas, pero fue con posterioridad a Saunderson. Que la historia se las asigne a Euler posiblemente est¨¦ provocado por la mayor difusi¨®n de los trabajos de ¨¦ste.

Respecto a los trabajos de Euler sobre este tema, destacan principalmente dos. Primero, sab¨ªa que el cuboide de aristas (44,117,240) era el m¨¢s peque?o posible. Y segundo, que si (x,y,z) son los lados de una caja de Euler, entonces los productos (yz,xz,xy) tambi¨¦n son los lados de otra caja de Euler. Estas cajas suelen llamarse cajas de Euler derivadas (o cuboides derivados).

Pero se puede ir a¨²n m¨¢s lejos. Los cuboides cumplen que sus cuatro diagonales espaciales (las diagonales internas que unen v¨¦rtices opuestos) son iguales. ?Por qu¨¦ no pedir que esa diagonal tambi¨¦n tenga longitud entera? Una caja que cumpla tambi¨¦n esa condici¨®n se llama cuboide perfecto.

Si prob¨¢is con la menor caja de Euler, la (44,117,240), ver¨¦is que ¨¦sta no es un cuboide perfecto. Y tambi¨¦n est¨¢ demostrado que las cajas de Euler (las que coment¨¢bamos antes que eran de Saunderson) tampoco son cuboides perfectos. Y, adem¨¢s, tambi¨¦n se sabe que las cajas de Euler derivadas tampoco pueden aspirar a ser cuboides perfectos (aqu¨ª ten¨¦is una demostraci¨®n de este resultado dada por John Leech en 1981). Por lo que si buscamos cajas perfectas en este sentido tendremos que orientar la b¨²squeda de otra forma.

Recapitulando, un cuboide perfecto es un cuboide en el que las longitudes de los lados, las diagonales de sus caras y la diagonal espacial son todas n¨²meros enteros positivos. Y ahora la pregunta est¨¢ clara: ?existen cuboides perfectos? Pues¡­no se sabe. Hasta ahora, no se ha encontrado ninguna caja perfecta ni tampoco se ha demostrado que no existan.

Se conocen algunos datos sobre ellas, como que si existen se debe cumplir que el lado menor debe medir m¨¢s de 10¹⁰, o algunas relaciones de divisibilidad que deben cumplir algunos lados o diagonales, pero no mucho m¨¢s.

Aunque hace relativamente poco se avanz¨® algo en el tema. No se encontr¨® ning¨²n cuboide perfecto, pero s¨ª se han encontrado paralelep¨ªpedos perfectos. La diferencia de ¨¦stos con los cuboides es que las caras no son todas rect¨¢ngulos o cuadrados, sino que son otro tipo de cuadril¨¢teros. Ello supone que las dos diagonales de cada cara sean distintas y que las cuatro diagonales espaciales sean tambi¨¦n distintas, por lo que en vez de necesitar 7 elementos enteros (los tres lados, las tres diagonales de las caras y la diagonal espacial) necesitamos 13 valores enteros: los tres lados, las seis diagonales de las caras (dos por cara) y las cuatro diagonales espaciales. Bien, pues aunque sean m¨¢s elementos los que deben ser enteros, para este tipo de cajas se encontraron ejemplos en el a?o 2010.

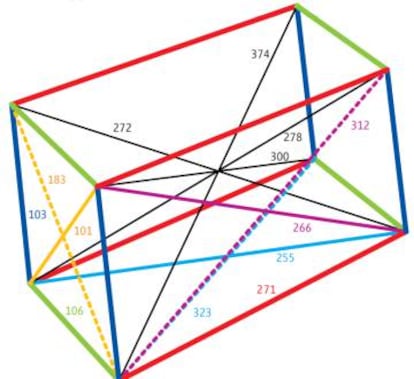
En la imagen ten¨¦is uno de ellos. Como se puede ver, las caras a izquierda y derecha son dos rombos de lados 103 y 106 que distan 271 (estos son los tres lados del paralelep¨ªpedo) cuyas diagonales miden (101,183); las diagonales del resto de caras son (266,312) y (255,323); y las diagonales espaciales miden (272,278,300,374). Como veis, los 13 valores son enteros positivos.

El hecho de encontrar un paralelep¨ªpedo perfecto fue una sorpresa, ya que se cre¨ªa que no exist¨ªa ninguno. Pero la sorpresa fue a¨²n mayor cuando se descubri¨® que ¨¦ste (que fue el primero que se descubri¨®) no era el ¨²nico: se conocen al menos 30 de estos paralelep¨ªpedos perfectos. Aqu¨ª ten¨¦is informaci¨®n sobre ello, aunque por desgracia el art¨ªculo no es de acceso p¨²blico. Pero para compensar esto, os dejo este otro art¨ªculo con mucha informaci¨®n sobre la b¨²squeda de los cuboides perfectos.

Como pod¨¦is ver, ciertos problemas sencillos de plantear y explicar (hasta un ni?o podr¨ªa entender su planteamiento) puede ser de inter¨¦s para matem¨¢ticos y tremendamente dif¨ªciles de resolver, y el que nos ha ocupado hoy es un buen ejemplo. Todav¨ªa no se han encontrado cuboides perfectos, ni se ha demostrado que no existan, por lo que seguimos, y posiblemente seguiremos durante mucho tiempo, en busca de la caja perfecta.