Manhattan, distancias y ¡°el juicio de Pit¨¢goras¡±

Creo que habr¨¢ poca discusi¨®n en el hecho de que la distancia, se entiende que la m¨¢s corta, entre dos puntos en una superficie plana es la l¨ªnea recta que une dichos puntos (aunque, recordemos, no sea la m¨¢s r¨¢pida). Por tanto, si queremos calcular la distancia entre dos puntos en una ciudad, simplemente tendremos que medir el segmento de recta que une dichos puntos.

Vale, la Tierra no es plana (de hecho, no se puede representar fielmente en un plano), pero lo que s¨ª es cierto que un ¡°trocito¡± peque?o (es decir, ¡°localmente¡±) s¨ª que ¡°se parece¡± a un plano, por lo que podemos hablar de la l¨ªnea recta de toda la vida en una ciudad y nos evitamos hablar de geod¨¦sicas y dem¨¢s.

Bueno, seguimos con lo que est¨¢bamos. Dec¨ªamos que la distancia entre dos puntos en una ciudad ser¨ªa lo que mida la l¨ªnea recta que une ambos puntos. Al menos eso dice la teor¨ªa, porque en la pr¨¢ctica normalmente no podremos ¡°recorrer¡± dicha l¨ªnea recta, a no ser que tengamos la inusual cualidad de atravesar paredes y edificios.

Pongamos un ejemplo. He tomado una imagen de La Carolina (Ja¨¦n) sacada de Google Maps y he marcado dos puntos en dos de las calles:

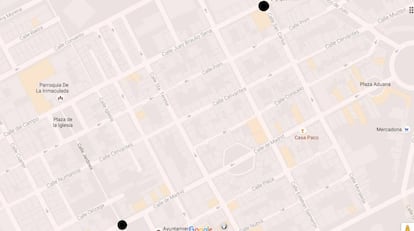
Aunque sobre el papel podr¨ªamos unirlos con una l¨ªnea recta (en rojo en la siguiente imagen), es evidente que en realidad no podr¨ªamos recorrer ese camino, por lo que tendr¨ªamos que ir recorriendo calles seg¨²n el propio mapa. En la imagen pod¨¦is ver dos de esos caminos posibles (en verde y en azul):

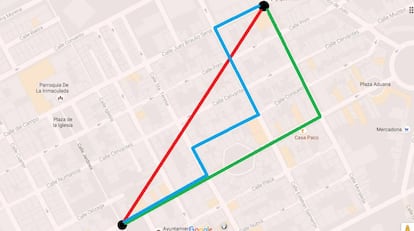
De hecho, esos dos caminos son m¨ªnimos, en el sentido de que ambos tienen longitud m¨ªnima en esta nueva manera de calcular la distancia. Esta manera de medir distancias se denomina distancia Manhattan, y, de forma m¨¢s general, nos dice cu¨¢l es la distancia entre dos puntos en una cuadr¨ªcula de ¡°calles¡± (l¨ªneas rectas) y ¡°edificios¡± (cuadros rodeados por l¨ªneas rectas), tipo ciudad (el nombre de Manhattan es, precisamente, por el dise?o en forma de cuadr¨ªcula que tienen la mayor¨ªa de sus calles).

Matem¨¢ticamente, si tomamos dos puntos p y q en una cuadr¨ªcula con coordenadas p=(p₁,p₂) y q=(q₁,q₂), la distancia Manhattan entre dichos puntos es la suma de los valores absolutos de las diferencias entre las coordenadas. Es decir:

d(p,q)=|q₁-p₁|+|q₂-p₂|

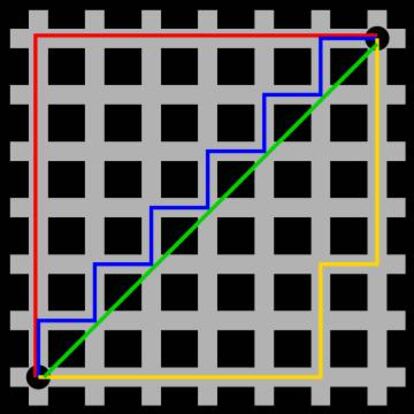
En la imagen, pod¨¦is ver una cuadr¨ªcula en la que tenemos dos puntos unidos con una l¨ªnea recta (en verde), que corresponde con la distancia habitual (la eucl¨ªdea), y varias maneras de unir ambos puntos con un camino m¨ªnimo siguiendo las calles de la cuadr¨ªcula (lo que ser¨ªa la distancia Manhattan entre ambos puntos). Pod¨¦is profundizar sobre este tema, conocido tambi¨¦n como geometr¨ªa taxicab, en este enlace.

Y ahora lo que se estar¨¢ preguntando m¨¢s de uno: ?qu¨¦ tiene que ver todo esto con un juicio? Vamos con la historia que me ha llevado a escribir este art¨ªculo.

Corr¨ªa el a?o 2002 cuando James Robbins es detenido precisamente en Manhattan, concretamente en la esquina de la Octava Avenida con la Calle 40, por venta de drogas. Adem¨¢s, su caso ten¨ªa como agravante que lo hizo a menos de 1000 pies de un colegio, el Holy Cross, situado en la Calle 43.

En un intento de eliminar dicho agravante, los abogados de Robbins echaron mano de la distancia Manhattan. En la imagen siguiente pod¨¦is ver los dos puntos, la esquina en la que detuvieron a Robbins y el colegio, y el camino de m¨ªnima distancia seg¨²n la distancia Manhattan:

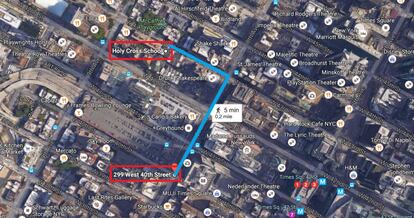
Tomar esta distancia como referencia eliminaba el agravante de los 1000 pies, ya que la longitud que separar¨ªa en este caso ambos puntos era de 1254 pies: los 764 pies que habr¨ªa que recorrer de la Octava Avenida antes de girar en ¨¢ngulo recto y los 490 pies que recorrer¨ªamos de la Calle 43 hasta llegar al Holy Cross.

Pero no sirvi¨®. El juez, entiendo yo, consider¨® que esa distancia m¨¢xima era de un radio de 1000 pies, por lo que habr¨ªa que calcular la longitud que separa ambos puntos en l¨ªnea recta. ?C¨®mo calcular dicha longitud? Pues con los datos anteriores es sencillo hacerlo utilizando el teorema de Pit¨¢goras. Los dos recorridos anteriores ser¨ªan los catetos de un hipot¨¦tico tri¨¢ngulo rect¨¢ngulo, por lo que la l¨ªnea recta que buscamos ser¨ªa la hipotenusa de dicho tri¨¢ngulo, como puede verse en la imagen siguiente:

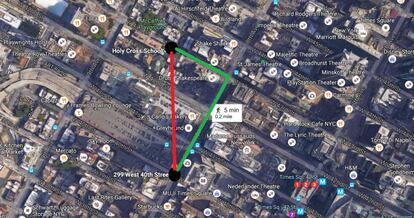
Usando este teorema, tenemos que 764²+490²=823796, cuya ra¨ªz cuadrada es 907.63 pies, que corresponde con la distancia en l¨ªnea recta entre ambos puntos. Como esta longitud es menor que 1000 pies, el agravante de proximidad no se pudo eliminar, y a Robbins le cayeron de 6 a 12 a?os de c¨¢rcel.

Este caso, supongo que por lo curioso del asunto, tuvo cierta relevancia en su momento, llegando a aparecer en el New York Times. Yo no conozco m¨¢s casos parecidos, en los que las matem¨¢ticas sean tan relevantes como para determinar la condena de un acusado, pero igual vosotros ten¨¦is informaci¨®n sobre alguno m¨¢s. Si es as¨ª, pod¨¦is utilizar los comentarios para hablarnos de ello.