Fermat y los pol¨ªgonos regulares

Si la semana pasada los protagonistas de El Aleph fueron los poliedros, en esta ocasi¨®n las estrellas del art¨ªculo van a ser sus ¡°hermanos¡± de dos dimensiones: los pol¨ªgonos. Y, m¨¢s concretamente, ser¨¢n los pol¨ªgonos regulares los que ejercer¨¢n de actores principales de nuestra historia de hoy. Pero antes de que estos pol¨ªgonos hagan acto de presencia, vamos a hablar brevemente de uno de los matem¨¢ticos m¨¢s importantes de la historia de las matem¨¢ticas: Pierre de Fermat.

Pierre de Fermat fue un jurista franc¨¦s del siglo XVII aficionado a las matem¨¢ticas que pasa por ser considerado el creador de la teor¨ªa de n¨²meros, aunque tambi¨¦n realiz¨® aportes en otras ¨¢reas de las matem¨¢ticas. Fermat sol¨ªa plantear resultados sin dar su demostraci¨®n, y no public¨® pr¨¢cticamente nada en vida. Sol¨ªa comunicar sus descubrimientos mediante cartas enviadas a otros matem¨¢ticos de la ¨¦poca (principalmente a Marin Mersenne), y deb¨ªa tener ¡°buen ojo¡± viendo que casi nunca se equivoc¨® en sus afirmaciones.

Y decimos ¡°casi¡± porque s¨ª cometi¨® alg¨²n error. El m¨¢s importante es, posiblemente, considerar que hab¨ªa encontrado una expresi¨®n que generaba siempre n¨²meros primos distintos. Fermat conjetur¨® que todos los n¨²meros de la forma 2 elevado a 2ⁿ m¨¢s 1 (el 1 se suma despu¨¦s de calcular las dos potencias de 2), llamados F_n, eran primos para todo n¨²mero entero no negativo que pudi¨¦ramos colocar en el lugar de n.

Cierto es que para 0, 1, 2, 3 y 4 esa expresi¨®n da n¨²meros primos, pero para n=5 el resultado es un n¨²mero compuesto. Fue Leonhard Euler quien, un siglo m¨¢s tarde, demostr¨® este hecho factorizando F₅. En la siguiente imagen pod¨¦is ver los resultados de F_n para n de 0 a 5 y la factorizaci¨®n de F₅:

Es decir, no todos estos n¨²meros de Fermat son primos (los que s¨ª lo son se denominan, como no pod¨ªa ser de otra forma, primos de Fermat). Pero la cosa es a¨²n m¨¢s grave: no se conoce ning¨²n otro n¨²mero de Fermat que sea primo aparte de F₀, F₁, F₂, F₃ y F₄.De alguno de los posteriores a F₅ se conoce su factorizaci¨®n (no son primos), y para alg¨²n otro se ha demostrado que no es primo, aunque todav¨ªa no se haya podido factorizar (dada la magnitud del n¨²mero en cuesti¨®n). Vamos, que no fue un error peque?o, sino que la afirmaci¨®n de Fermat en este tema fue un fallo bastante gordo.

Pero, como todo lo que tocaba Fermat, estos n¨²meros escond¨ªan algo realmente interesante, una relaci¨®n inesperada con una figuras planas que, en principio, no tienen mucho que ver con ellos: los pol¨ªgonos regulares.

Un pol¨ªgono es una figura plana formada por un n¨²mero finito de segmentos, que se llaman lados, que forman una cadena cerrada y que delimitan una regi¨®n del plano. Los puntos en los que se cortan dos segmentos se llaman v¨¦rtices. Un cuadrado, un tri¨¢ngulo, un rect¨¢ngulo o un pent¨¢gono son ejemplos de pol¨ªgonos.

Si los lados del pol¨ªgono son iguales y los ¨¢ngulos que forman cada dos lados consecutivos tambi¨¦n lo son, entonces estamos ante un pol¨ªgono regular. Un cuadrado y un tri¨¢ngulo equil¨¢tero son pol¨ªgonos regulares.

La construcci¨®n de pol¨ªgonos regulares con regla y comp¨¢s, siguiendo las normas griegas que ya comentamos cuando hablamos de la cuadratura del c¨ªrculo, ha sido un tema tratado por muchos matem¨¢ticos desde la antig¨¹edad. Desde hace mucho tiempo se sabe c¨®mo construir de esta forma un tri¨¢ngulo equil¨¢tero, un cuadrado o un pent¨¢gono, pero, por ejemplo, no se conoc¨ªa en la ¨¦poca de Fermat ninguna manera de construir un hept¨¢gono regular (siete lados) o un ene¨¢gono regular (nueve lados). De hecho, no se sab¨ªa si pod¨ªan construirse todos, y, en el caso de que no se pudiera, no hab¨ªa una forma de determinar cu¨¢les eran construibles con regla y comp¨¢s y cu¨¢les no.

Pero lleg¨® Carl Friedrich Gauss y revolucion¨® el tema. En su maravillosa obra Disquisitiones Arithmeticae, Gauss demostr¨® que si el n¨²mero de lados de un pol¨ªgono cumpl¨ªa cierta condici¨®n, entonces era construible con regla y comp¨¢s. Esa condici¨®n era que la factorizaci¨®n en n¨²meros primos del n¨²mero de lados s¨®lo pod¨ªa ser una potencia de 2, un primo de Fermat o un producto de estos tipos de n¨²meros: una potencia de 2 por un primo de Fermat, un producto de varios primos de Fermat distintos o la multiplicaci¨®n de una potencia de 2 por varios primos de Fermat tambi¨¦n distintos.

Escrito de manera m¨¢s ¡°matem¨¢tica¡±, Gauss demostr¨® lo siguiente en la secci¨®n VII de sus Disquisitiones:

Si el n¨²mero de lados, n, de un pol¨ªgono regular es de la forma n=2^r ¡¤ p₁ ¡¤ ¡­ ¡¤ p_k, con r un entero mayor o igual que cero y p₁, ¡­, p_k primos de Fermat distintos, entonces dicho pol¨ªgono regular es construible con regla y comp¨¢s.

Aclaro que podr¨ªa no aparecer ning¨²n primo de Fermat en la descomposici¨®n, y recalco de nuevo que si aparece m¨¢s de uno entonces deben ser distintos. Obviando ahora los casos que no tienen sentido (r=0 sin primos de Fermat dar¨ªa un pol¨ªgono de un lado, y r=1 sin primos de Fermat dar¨ªa un pol¨ªgono de dos lados), con este resultado hemos avanzado bastante en lo que se refiere a identificar los pol¨ªgonos regulares construibles¡­

¡­pero todav¨ªa no est¨¢ todo hecho. Si el n¨²mero de lados tiene esa forma, entonces el pol¨ªgono regular es construible, pero si no es de esa forma no sabemos nada todav¨ªa. Lo ideal ser¨ªa que dicho resultado tambi¨¦n fuera cierto al contrario, ?verdad? Es decir, que tambi¨¦n fuera cierto que si un pol¨ªgono regular es construible, entonces su n¨²mero de lados sigue esa expresi¨®n.

Gauss pensaba que s¨ª, que esto tambi¨¦n se cumpl¨ªa, pero no lleg¨® a demostrarlo (al menos no se conoce ninguna demostraci¨®n suya al respecto). Lo importante es que no se equivocaba: Pierre Wantzel, en 1837, demostraba que el rec¨ªproco del resultado de Gauss tambi¨¦n era cierto. Esto s¨ª que cierra completamente el c¨ªrculo: un pol¨ªgono regular es construible con regla y comp¨¢s si y s¨®lo si su n¨²mero de lados factoriza en n¨²meros primos de la forma comentada antes.

Esto significa que, con las reglas cl¨¢sicas griegas, podemos construir un cuadrado (2² lados), un tri¨¢ngulo equil¨¢tero (3 lados, primo de Fermat), un pent¨¢gono regular (5 lados, primo de Fermat), un hex¨¢gono regular (2¡¤3 lados, producto de potencia de 2 por primo de Fermat) o un dec¨¢gono regular (2¡¤5 lados, potencia de 2 por primo de Fermat), pero no un hept¨¢gono regular ni un ene¨¢gono regular, ya que ninguno factoriza de la forma descrita.

Comentario aparte merece el heptadec¨¢gono regular, pol¨ªgono regular de 17 lados (primo de Fermat). Gauss, cuando ten¨ªa ??19 a?os!!, demostr¨® que este pol¨ªgono era construible con regla y comp¨¢s, pero no dio los pasos de su construcci¨®n. Fue Jonathan Erchinger quien nos mostr¨® c¨®mo construir un heptadec¨¢gono regular en 64 pasos. Y tambi¨¦n el pol¨ªgono regular de 65537 lados (primo de Fermat), cuya construcci¨®n fue desarrollada, durante 10 a?os, por Johann Gustav Hermes. La public¨® en 1894 y consta de nada menos que 200 p¨¢ginas.

Viendo la factorizaci¨®n del n¨²mero de lados de los pol¨ªgonos regulares construibles, es evidente que se pueden construir infinitos de ellos con regla y comp¨¢s. Pero analizando el asunto m¨¢s profundamente, y teniendo en cuenta que no se conocen m¨¢s primos de Fermat que F₀, F₁, F₂, F₃ y F₄, en esencia son muy pocos los pol¨ªgonos regulares construibles. De hecho, si quitamos la potencia de 2 tenemos solamente 31 pol¨ªgonos regulares que sabemos que son construibles. Mientras no se descubran m¨¢s primos de Fermat, ¨¦stos ser¨¢n los ¨²nicos de lados impares que podremos aspirar a construir. Cuando menos curioso que, te¨®ricamente (en la pr¨¢ctica es pr¨¢cticamente imposible), podamos construir con regla y comp¨¢s un pol¨ªgono regular de?4294967295 lados (3¡¤5¡¤17¡¤257¡¤65537) pero no podamos construir uno de 7 lados...

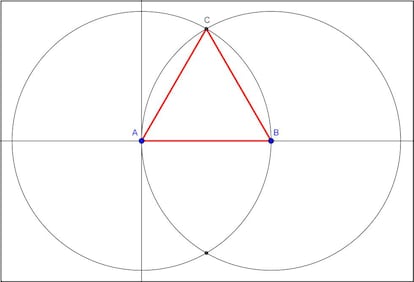
Para terminar, os animo a que expliqu¨¦is en los comentarios c¨®mo construir¨ªais con regla y comp¨¢s (y las reglas cl¨¢sicas, tenedlo en cuenta) alg¨²n pol¨ªgono regular. Considerad que comenz¨¢is con unos ejes y dos puntos, el origen, A, y otro punto, B, en el eje horizontal. Os dejo yo la m¨¢s sencilla: la construcci¨®n de un tri¨¢ngulo equil¨¢tero:

Trazamos una circunferencia con centro A y radio AB, y otra circunferencia con centro B y radio tambi¨¦n AB. Esas dos circunferencias se cortan en dos puntos. Tomamos, por ejemplo, el superior, C, y trazamos los segmento AB, AC y BC. Esos tres segmentos forman un tri¨¢ngulo equil¨¢tero.

Aqu¨ª ten¨¦is una imagen con la construcci¨®n: