Pelos, saludos y palomas

?Hay en Espa?a dos personas que tengan exactamente el mismo n¨²mero de pelos en la cabeza? Esta extra?a pregunta, y otras m¨¢s o menos curiosas, pueden responderse utilizando un resultado matem¨¢tico que destaca por su extremada sencillez: el principio del palomar.

El principio del palomar dice b¨¢sicamente que si tenemos que colocar unas cuantas palomas en palomares y tenemos m¨¢s palomas que palomares, entonces en (al menos) un palomar habr¨¢ m¨¢s de una paloma.

Evidente a la par que sencillo, ?verdad? Pues, a pesar de ello, este resultado, atribuido a Dirichlet, es muy ¨²til para resolver cierto tipo de cuestiones num¨¦ricas, como la que coment¨¢bamos al principio. Pero antes de ir a ella vamos a plantear otras cuestiones que tambi¨¦n se puede resolver con este principio.

Comenzamos con la siguiente, eminentemente num¨¦rica:

Demuestra que si escogemos tres n¨²meros naturales cualesquiera (naturales: 1, 2, 3, 4, 5,¡­), siempre se cumple que habr¨¢ dos de ellos cuya resta es m¨²ltiplo de 2.

Esto es f¨¢cil de demostrar sin usar el principio del palomar con un simple an¨¢lisis de todas las opciones posibles:

- Si hemos escogido tres impares, cualquier pareja tiene como resta un n¨²mero par, y por tanto m¨²ltiplo de 2.

- Si hemos escogido dos impares y un par, la resta de los dos impares da un n¨²mero par, m¨²ltiplo de 2.

- Si hemos escogido un impar y dos pares, la resta de los pares da un n¨²mero par, tambi¨¦n m¨²ltiplo de 2.

- Y si hemos escogido tres pares, la resta de cualesquiera dos de ellos da un n¨²mero par, que vuelve a ser entonces m¨²ltiplo de 2.

Ahora, imaginad que escogemos 1000 n¨²meros naturales y nos piden que demostremos que al menos dos de ellos cumplen que su resta es m¨²ltiplo de 999. Ahora ser¨ªa una locura analizar todas las opciones, por lo que necesitamos otra estrategia. Vamos a usar el principio del palomar.

Al dividir un n¨²mero natural entre 999, podemos obtener como resto de la divisi¨®n cualquier n¨²mero entre 0 y 998, que son 999 restos distintos. Si dividimos nuestros 1000 n¨²meros entre 999, obtendremos 1000 restos (uno por cada n¨²mero). Tomando esos 1000 n¨²meros como las palomas y los 999 restos distintos como los palomares, tenemos que al menos dos n¨²meros dejar¨¢n el mismo resto al dividir entre 999.

Si llamamos M y N a esos dos n¨²meros, tenemos entonces que M=999¡¤P+R y que N=999¡¤Q+R (distintos cocientes pero mismo resto). Si restamos llegamos a lo siguiente:

M-N=(999¡¤P+R)-(999¡¤Q+R)=999¡¤P+R-999¡¤Q-R=999¡¤P-999¡¤Q=999¡¤(P-Q)

Es decir, su resta es m¨²ltiplo de 999. Usando el principio del palomar, hemos demostrado que entre nuestros 1000 n¨²meros naturales siempre habr¨¢ al menos dos cuya resta ser¨¢ m¨²ltiplo de 999.

Vamos ahora con otro problema, geom¨¦trico en este caso:

Tomamos un tri¨¢ngulo equil¨¢tero de lado 2. Demostrar que si tomamos 5 puntos dentro de ¨¦l, siempre ocurrir¨¢ que al menos dos estar¨¢n a una distancia menor que 1.

Est¨¢ claro que cada pareja de puntos estar¨¢ a una distancia menor que 2, pero lo que no est¨¢ claro en un principio es si podremos encontrar dos a distancia menor que 1. ?Y si los colocamos muy cerca de los bordes lo m¨¢s separados que podamos?

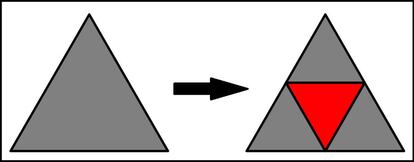
Bien, la cosa es sencilla. Tomamos los puntos medios de los lados de nuestro tri¨¢ngulo y los unimos como muestra la imagen, quedado as¨ª dividido nuestro tri¨¢ngulo equil¨¢tero en cuatro tri¨¢ngulos equil¨¢teros iguales de lado 1:

Considerando a los 5 puntos a colocar como las palomas y los 4 tri¨¢ngulos de lado 1 como los palomares, est¨¢ claro que al menos dos de ellos caer¨¢n dentro del mismo triangulito de lado 1, y por tanto estar¨¢n a distancia menor que 1 (si alguno de ellos cae justo en alguna de las l¨ªneas creadas para formar el tri¨¢ngulo central, se puede ver f¨¢cilmente que el resultado tambi¨¦n se cumple).

Seguro que despu¨¦s de ver el enunciado del principio del palomar y los ejemplos anteriores, a muchos ya se os habr¨¢ ocurrido c¨®mo usarlo para responder a la pregunta que lanz¨¢bamos al comienzo de este art¨ªculo, pero por si acaso no es as¨ª lo vamos a explicar.

Si consultamos el art¨ªculo de la Wikipedia dedicado al pelo, podemos encontrar una aproximaci¨®n a la cantidad de pelos que un adulto tiene en la cabeza:

El pelo se distribuye en casi toda la superficie corporal, exceptuando las superficies palmoplantares, el ombligo y las mucosas. En un adulto el n¨²mero aproximado de pelos es de unos cinco millones, reparti¨¦ndose en forma desigual a lo largo del cuerpo. En la cabeza hay alrededor de un mill¨®n, encontr¨¢ndose entre 100000 y 150000 en el cuero cabelludo.

Se entiende que ese mill¨®n cuenta los del cuero cabelludo, la barba, la nariz, etc. Con este dato, y teniendo en cuenta que, seg¨²n el INE, a 1 de julio de 2016 Espa?a ten¨ªa 46468102 habitantes, ya podemos responder a nuestra pregunta. Si tomamos esos m¨¢s de 46 millones de habitantes como las palomas y todas las posibles cantidades de pelos, 1 mill¨®n, como palomares, tenemos que seguro que habr¨¢ al menos dos personas con la misma cantidad de pelos en su cabeza (al haber m¨¢s palomas que palomares). De hecho, estamos seguros de que podemos encontrar al menos 47 personas con la misma cantidad de pelos repartidos por su cabeza. Sencillo a la par que curioso.

Y ya que estamos con preguntas peculiares, vamos con otra. Imaginad que el pr¨®ximo fin de semana asist¨ªs a una gran fiesta, y supongamos que os junt¨¢is 5000 personas. Algunos de los asistentes os conocer¨¦is entre vosotros y otros no, como es natural, y algunos conocer¨¢n a m¨¢s gente que otros. Bien, pues es seguro que habr¨¢ al menos dos asistentes a la fiesta que conocer¨¢n al mismo n¨²mero de personas.

?Tambi¨¦n se puede demostrar esto con el principio del palomar? Pues s¨ª, tambi¨¦n se puede demostrar esto con el principio del palomar, y vamos a verlo ahora mismo. Las palomas van a ser las personas que asisten a la fiesta, 5000, y los palomares ser¨¢n las posibles cantidades de personas que puede conocer alguien. En principio, hay tambi¨¦n 5000 posibilidades en lo que se refiere a conocer gente, ya que ese ¡°alguien¡± podr¨ªa conocer a 0 personas, a 1 persona, a 2 personas, y as¨ª hasta 4999 personas (que se conozca a uno mismo se obvia)¡­

¡­pero hay un peque?o detalle que nos permite usar nuestro principio. Si alguien no conoce a nadie en la fiesta, entonces no puede darse el caso de que otro asistente conozca a los otros 4999 ¡°fiesteros¡±, porque entonces tambi¨¦n conocer¨ªa a nuestro ¡°alguien¡±. Por tanto, 0 y 4999 no pueden darse a la vez. Descartando uno de ellos (da igual el que sea), tenemos 4999 cantidades de personas que se pueden conocer, 4999 palomares. Como hay m¨¢s palomas (personas) que palomares (personas que alguien puede conocer), al menos habr¨¢ dos asistentes a la fiesta que conocer¨¢n al mismo n¨²mero de personas.

Como hemos visto con estos ejemplos, no hay que subestimar la potencia de un resultado matem¨¢tico por muy simple y evidente que pueda parecer en un primer contacto, como ocurre con el principio del palomar. Y los ejemplos que hemos comentado no son ni mucho menos los ¨²nicos para los que este resultado tiene utilidad. Estoy seguro que algunos de vosotros conoc¨¦is m¨¢s casos curiosos e interesantes, y espero que nos habl¨¦is de ellos en los comentarios.