Las matem¨¢ticas de la f¨®rmula de puntuaci¨®n de ex¨¢menes test

Estoy seguro de que todos los que est¨¢is leyendo este art¨ªculo hab¨¦is hecho en alguna ocasi¨®n un examen tipo test durante vuestra vida acad¨¦mica. Si hac¨¦is memoria, seguro que recordar¨¦is que en esos ex¨¢menes todos nos preocup¨¢bamos por saber cosas como si las preguntas que dej¨¢bamos en blanco nos iban a restar puntuaci¨®n o cu¨¢nto nos iba a penalizar una pregunta fallada. Hab¨ªa veces en las que esos fallos no restaban (es raro, pero conozco alg¨²n caso), pero lo normal era lo contrario. Lo curioso era que no siempre restaban lo mismo. Hoy vamos a hablar sobre cu¨¢l ser¨ªa la f¨®rmula correcta para puntuar en un test, y vamos a explicarlo matem¨¢ticamente.

Asumiendo que las preguntas en blanco ni suman ni restan, lo primero que hay que dejar claro es que lo m¨¢s conveniente es que las preguntas falladas resten puntuaci¨®n. La raz¨®n es muy sencilla: penalizar a quien responde al azar. El gran peligro de los ex¨¢menes test es que alguien que no tiene ni idea de la materia puede aprobar si tiene suerte (la famosa quiniela), por lo que tenemos que intentar minimizar la influencia de esa suerte.

Ahora, suponiendo que hay una ¨²nica respuesta correcta por pregunta y que todas las preguntas tienen la misma importancia (es decir, todos los fallos restan lo mismo), ?cu¨¢nto debe restar cada fallo? Pues¡­depende. No es lo mismo un examen test en el que cada pregunta tiene dos posibles opciones de respuesta que otro en el que las opciones son cinco. Respondiendo al azar, en el primero caso tenemos mayor probabilidad de acertar, 1/2, que en el segundo, 1/5, por lo que en el primero caso debe restar m¨¢s que en el segundo.

Por tanto, parece l¨®gico que la penalizaci¨®n por pregunta fallada debe tener alguna relaci¨®n con el n¨²mero de opciones de respuesta que tenemos en cada pregunta. Ya hemos dado el primer paso.

Sigamos con esta persona ficticia que no tiene ni idea de los contenidos sobre los que versa nuestro examen y que, por tanto, responde totalmente al azar. Suponiendo que contesta todas las preguntas, ?qu¨¦ nota queremos que saque? Pues est¨¢ bastante claro, ?verdad? Queremos que alguien que responde todas las preguntas al azar espere sacar un 0 bien redondito (fijaos en la palabra en cursiva de la frase anterior, espere). Aunque se puede dar el caso de que un examen test d¨¦ una puntuaci¨®n negativa, debemos aplicar una f¨®rmula que cumpla que la nota esperada (atentos de nuevo a la palabra en cursiva) para quien responde todo al azar sea un 0.

Vamos a dar la f¨®rmula que se debe usar para puntuar en un test y despu¨¦s explicaremos matem¨¢ticamente por qu¨¦ es as¨ª. Si cada pregunta del examen tiene k posibles respuestas, la f¨®rmula que debe utilizar para puntuar es la siguiente:

Esto significa que, si en nuestro test hay 3 posibles respuestas por pregunta, cada error debe restar 0¡¯5; si tiene 4 posibles respuestas, cada error debe restar 0¡¯33¡­; con 5 opciones por pregunta, un error debe restar 0¡¯25; y as¨ª sucesivamente.

El porqu¨¦ de esa f¨®rmula tiene que ver con esas palabras en cursiva que destac¨¢bamos unos p¨¢rrafos m¨¢s arriba: espere y esperada. Como queremos que la persona que no sabe nada saque un cero, partimos de que las preguntas se responden de manera aleatoria. Por ello, la nota de cada pregunta es lo que se llama una variable aleatoria (discreta en este caso) que puede tener dos valores (con distintas probabilidades) dependiendo de si la respuesta es acertada (obteniendo as¨ª un 1) o err¨®nea (restando as¨ª una cierta cantidad todav¨ªa por determinar).

Como la nota final del examen es la suma de las notas de cada una de las preguntas, la nota tambi¨¦n es una variable aleatoria, definida como la suma de las variables aleatorias ¡°notas de cada una de las preguntas¡±. Y la nota esperada en el examen se obtiene mediante una medida que se le puede calcular a una variable aleatoria que se denomina esperanza.

Esto que parece un poco l¨ªo en realidad es bastante m¨¢s sencillo. Vamos a ponerle nombre a todas las caracter¨ªsticas de nuestro examen. Supongamos que tenemos N preguntas y que n_i es la nota obtenida en la pregunta i (la nota que sacamos en una pregunta concreta). Esa nota tiene dos posibles valores, dependiendo de si acertamos o fallamos. Si acertamos tendremos un 1, y si fallamos se nos restar¨¢ algo. Si llamamos p a lo que se resta por fallo, la nota al errar ser¨ªa ¨Cp. Lo que queremos es calcular cu¨¢nto vale p, cu¨¢nto se nos resta por fallar una pregunta.

Si, como dijimos antes, cada pregunta tiene k posibles respuestas, tenemos que la probabilidad de acertar al responder de manera aleatoria es 1/k y la probabilidad de fallar es 1-1/k. Ya tenemos todos los datos para definir la variable aleatoria n_i=¡±nota sacada en la pregunta i¡±:

Calculemos ahora la nota esperada en cada pregunta, la esperanza de la variable aleatoria n_i. Esta esperanza se calcula multiplicando valor por probabilidad y sumando los resultados, por lo que:

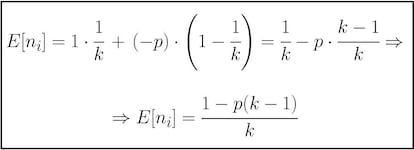
Si ahora tomamos la variable aleatoria NOTA=¡±nota final del examen¡±, est¨¢ claro que estar¨¢ definida como la suma de las notas de cada una de las preguntas. Y como queremos calcular la nota esperada en el examen, vamos a calcular la esperanza de esta nueva variable aleatoria (aqu¨ª usamos la linealidad de la esperanza, que nos dice que la esperanza de la suma es igual a la suma de las esperanzas). Teniendo tambi¨¦n en cuenta que todas las variables aleatorias asociadas a la nota de cada pregunta tienen la misma esperanza (no depende de la pregunta), tenemos lo siguiente:

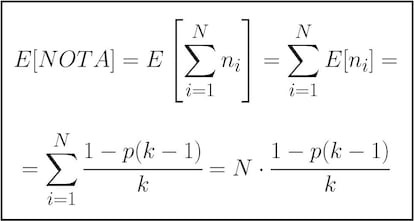
La expresi¨®n que hemos obtenido es la nota esperada en el examen si respondemos todas las preguntas de manera aleatoria. Como queremos que esa nota esperada sea un buen 0, igualamos a cero y despejamos lo ¨²nico que no conocemos, lo que nos resta cada pregunta fallada, p:

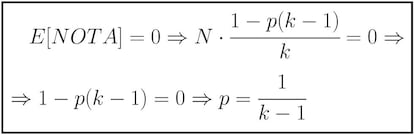
Por tanto, cada pregunta fallada debe restar el resultado de dividir 1 entre el n¨²mero de opciones menos uno, quedando entonces la f¨®rmula para el c¨¢lculo de la puntuaci¨®n como coment¨¢bamos antes:

?Conoc¨ªas la f¨®rmula? ?Y la explicaci¨®n matem¨¢tica de la misma? ?Has hecho alg¨²n examen test en el que te hayan puntuado con ella? ?Y alguno en el que las condiciones de puntuaci¨®n eran otras? Cu¨¦ntanos tu experiencia en los comentarios.

Quiero agradecer a varios de mis compa?eros de trabajo que el otro d¨ªa sacaran este tema. La conversaci¨®n que tuvimos me hizo ver que podr¨ªa ser interesante escribir sobre ello.