La maravillosa armon¨ªa que esconden los cuadrados m¨¢gicos

Lo confieso: soy un enamorado de los cuadrados m¨¢gicos. Y lo soy desde siempre, desde la primera vez que vi uno, desde el primer momento en el que tuve la fortuna de conocer la maravillosa armon¨ªa que esconden esas cajitas de n¨²meros aparentemente colocados al azar. Aunque ahora mismo no sabr¨ªa decir exactamente en qu¨¦ momento de mi vida se produjo ese primer contacto con los cuadrados m¨¢gicos, mi fascinaci¨®n por estos objetos matem¨¢ticos comenz¨® ah¨ª y, puedo asegurar, continuar¨¢ hasta el fin de mis d¨ªas. Espero que con este art¨ªculo pueda contagiaros al menos una peque?a parte de este particular amor tanto a los que ya los conoc¨¦is como a los que no.

Definir cuadrado m¨¢gico es sencillo: es un cuadrado de n¨²meros en el que todas las filas, todas las columnas y sus dos diagonales suman la misma cantidad, llamada constante m¨¢gica. Entre ellos, podr¨ªa decirse que los m¨¢s especiales son los que contienen una cierta cantidad de n¨²meros enteros positivos consecutivos comenzando en el 1. Suponiendo que nuestro cuadrado m¨¢gico tiene n filas y n columnas, ¨¦stos ser¨ªan los que contienen los n¨²meros enteros positivos desde el 1 hasta el n². Por ejemplo, aqu¨ª ten¨¦is uno de estos cuadrados m¨¢gicos con 4 filas y 4 columnas:

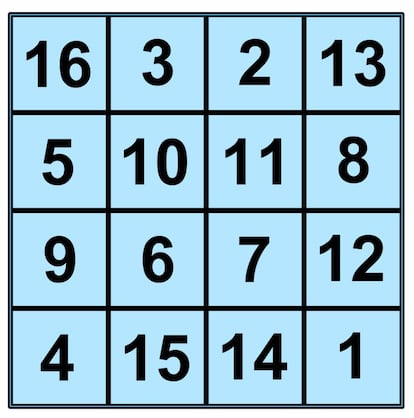
Pod¨¦is ver que todas las filas, todas las columnas y las dos diagonales suman 34, que ser¨ªa entonces la constante m¨¢gica del cuadrado. En general, para estos cuadrados m¨¢gicos especiales tenemos una f¨®rmula para calcular dicha constante m¨¢gica. Siendo n el n¨²mero de filas y de columnas, esta constante es n(n²+1)/2.

Por cierto, ¨¦ste no es el ¨²nico cuadrado m¨¢gico de orden 4. De hecho hay 880 cuadrados m¨¢gicos de este tama?o (lo calcul¨® Frenicle de Bessy en 1693). Por completar esto, hay un ¨²nico cuadrado m¨¢gico de orden 1, no hay ninguno de orden 2 (?sabr¨ªas demostrarlo?), hay solamente un cuadrado m¨¢gico de orden tres (salvo rotaciones y reflexiones) y exactamente 275305224 cuadrados m¨¢gicos de orden 5. Para ¨®rdenes superiores no se sabe con exactitud cu¨¢ntos hay.

En lo que se refiere a su historia, simplemente comentar¨¦ que en el tercer milenio a. C. en China ya se conoc¨ªan, y que otras civilizaciones antiguas como los egipcios, los griegos o lo ¨¢rabes tambi¨¦n tuvieron conocimiento de su existencia, atribuy¨¦ndoles habitualmente propiedades m¨ªsticas. Seg¨²n lo que sabemos, los cuadrados m¨¢gicos llegaron a Europa alrededor del siglo XIV, y muchos de los grandes matem¨¢ticos posteriores a esta fecha se interesaron por ellos.

Conocemos algoritmos para construir cuadrados m¨¢gicos de cualquier orden.

Pero dejemos hoy a un lado la historia y vayamos al turr¨®n: ?sabemos construir cuadrados m¨¢gicos? Esto es, ?tenemos alg¨²n algoritmo mediante el cual podamos construir cuadrados m¨¢gicos? Pues s¨ª, sabemos, y adem¨¢s podemos construir cuadrados m¨¢gicos de cualquier orden, aunque el m¨¦todo de construcci¨®n depende de cu¨¢l sea este orden.

Cuadrados m¨¢gicos de orden impar

Para este tipo de cuadrados m¨¢gicos se conocen varios m¨¦todos de construcci¨®n. El que aqu¨ª vamos a contar se denomina m¨¦todo de Loub¨¨re, y se debe al matem¨¢tico franc¨¦s Simon de la Loub¨¨re. Este m¨¦todo es como sigue:

Colocamos el 1 en la posici¨®n central de la fila superior, y despu¨¦s, a partir del 1 y en orden creciente, vamos colocando el resto de n¨²meros en diagonal. Si en alg¨²n momento nos toca colocar un n¨²mero en una posici¨®n ya ocupada, colocamos dicho n¨²mero debajo del que hab¨ªamos colocado justo antes.

Como lo de la colocaci¨®n en diagonal a veces puede ser algo liosa, os doy un truco: si un n¨²mero se ha colocado en la posici¨®n de la fila p y la columna q, posici¨®n (p,q), el siguiente se coloca en la posici¨®n (p-1,q+1), teniendo en cuenta que si nos pasamos de n volvemos a 1 y bajamos de 1 volvemos a n. Si esa posici¨®n est¨¢ ocupada, colocamos el n¨²mero debajo de la posici¨®n (p,q).

Veamos c¨®mo usar este m¨¦todo para construir un cuadrado m¨¢gico de orden 5. Comenzamos con el 1 en la posici¨®n (1,3); el 2 ir¨¢ en la (5,4); el 3 en la (4,5); el 4 en la (3,1); el 5 en la (2,2); el 6 deb¨ªa ir en la (1,3), pero como est¨¢ ocupada (por el 1) lo colocamos debajo del 5, en la posici¨®n (3,2); el 7 ir¨ªa ahora en la (2,3); el 8 en la (1,4); el 9 en la (5,5); el 10 en la (4,1); el 11 ir¨ªa en la (3,2), pero ah¨ª ya est¨¢ el 6, por lo que lo colocamos debajo del 10, en la posici¨®n (5,1); y as¨ª sucesivamente. Nos quedar¨ªa el siguiente cuadrado m¨¢gico:

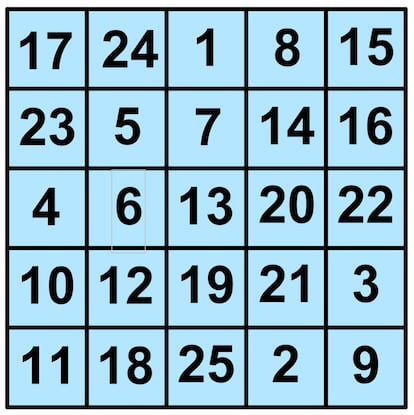
Pod¨¦is comprobar que todas las filas, todas las columnas y las dos diagonales suman 65, que es la constante m¨¢gica de estos cuadrados m¨¢gicos de orden 5.

Vayamos ahora con los de orden par. En este caso, debemos distinguir dos casos: los que tienen orden 4k (4, 8, 12, 16, 20¡­) y los que tienen orden 4k+2 (6, 10, 14, 18, 22¡­).

Cuadrados m¨¢gicos de orden 4k

Para construir este tipo de cuadrados m¨¢gicos, vamos a hacer lo siguiente:

Colocamos los n¨²meros desde el 1 hasta el n por filas en orden creciente. Despu¨¦s, dejamos tal cual el cuadrado central de orden n/2 y los cuadrados de las esquinas de orden n/4.Y ahora intercambiamos los que quedan arriba con los que quedan abajo, coloc¨¢ndolos en orden decreciente, y los que quedan a la izquierda con los que quedan a la derecha, invirtiendo tambi¨¦n el orden. El cuadrado resultante es un cuadrado m¨¢gico de orden 4k.

Por si la cosa no ha quedado muy clara, vamos a construir como ejemplo un cuadrado m¨¢gico de orden 8. A la izquierda pod¨¦is ver el cuadrado inicial, con los n¨²meros colocados en filas en orden creciente y en el que hemos destacado los n¨²meros que cambiaremos mediante un fondo amarillo (los que tienen fondo azul ser¨¢n los que dejaremos donde est¨¢n). A la derecha ten¨¦is el cuadrado m¨¢gico que nos queda al intercambiar como hemos descrito antes:

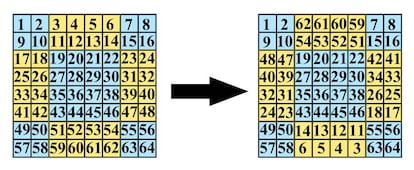
Cuadrados m¨¢gicos de orden 4k+2

Los m¨¦todos de construcci¨®n de estos cuadrados m¨¢gicos son algo m¨¢s complejos. Como el art¨ªculo ya tiene bastante informaci¨®n, os dejo enlaces a dos de ellos para que quien est¨¦ interesado los pueda consultar:

¡¤ M¨¦todo LUX, debido a John Horton Conway.

¡¤ M¨¦todo Strachey.

Como coment¨¢bamos al principio del art¨ªculo, ¨¦stos cuya construcci¨®n hemos descrito son especiales porque llevar dentro de ellos n¨²meros consecutivos a partir del 1. Pero hay muchos m¨¢s, con n¨²meros con caracter¨ªsticas muy especiales y hasta con elementos que no son n¨²meros. De ellos hablaremos en otra ocasi¨®n.

Y para finalizar este art¨ªculo sobre cuadrados m¨¢gicos, volvamos al 4x4 que os ense?aba unos p¨¢rrafos m¨¢s arriba:

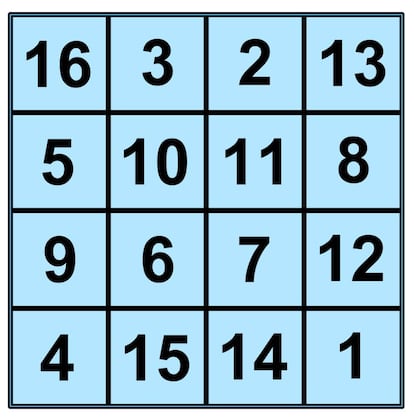
Este cuadrado m¨¢gico es muy famoso por aparecer en la obra Melancol¨ªa I de Alberto Durero, parte del cual ilustra este art¨ªculo. Aqu¨ª ten¨¦is una imagen de la obra al completo:

Y es tremendamente interesante por muchas cosas. Como hab¨ªamos visto antes, la constante m¨¢gica de este cuadrado es 34: todas las filas, todas las columnas y las dos diagonales suman 34. Sumad las esquinas. Os da 34, ?verdad? Sumad ahora los cuatro n¨²meros centrales: da 34. Sumemos los dos centrales de la fila de arriba con los dos centrales de la fila de abajo: 34. ?Y los dos centrales de la columna de la izquierda con los dos centrales de la columna de la derecha? Correcto: 34. Si lo dividimos en cuatro cuadrados 2x2, en todos los casos sus elementos suman 34, y hay muchas otras agrupaciones sim¨¦tricas de n¨²meros de cuatro en cuatro que, efectivamente, suman 34. Os animo a que las busqu¨¦is y a que nos lo cont¨¦is en los comentarios.

Espero que os haya gustado esta peque?a gran introducci¨®n a los cuadrados m¨¢gicos, y os invito a que intent¨¦is construir alg¨²n otro con las reglas que hemos contado en este art¨ªculo. Si ten¨¦is alg¨²n problema con estas construcciones no ten¨¦is m¨¢s que comentarlo. Y si conoc¨¦is alg¨²n otro m¨¦todo de construcci¨®n de cuadrados m¨¢gicos que no hayamos comentado aqu¨ª, estaremos muy agradecidos si nos lo quer¨¦is describir en un comentario. Muchas gracias a todos.