No solo de n¨²meros consecutivos vive el cuadrado m¨¢gico

En el art¨ªculo de la semana pasada habl¨¢bamos sobre cuadrados m¨¢gicos. En aquella ocasi¨®n, nos centramos en los cuadrados m¨¢gicos que contienen n¨²meros consecutivos desde 1 en adelante (hasta n² si el cuadrado tiene n filas y n columnas), pero coment¨¢bamos que hab¨ªa muchos otros tipos. El mundo de los cuadrados m¨¢gicos es mucho m¨¢s variado, y hoy vamos a ver unos cuantos ejemplos de esta variedad.

En los cuadrados m¨¢gicos num¨¦ricos, no siempre se cumple que todos los n¨²meros son distintos. Es evidente que si todos los n¨²meros son iguales, el cuadrado resultante es trivialmente m¨¢gico, pero repitiendo s¨®lo algunos aparecen tambi¨¦n cosas interesantes. Uno de los ejemplos m¨¢s conocidos de este tipo de cuadrados m¨¢gicos es que aparece en la llamada Fachada de la Pasi¨®n de La Sagrada Familia de Barcelona. Es ¨¦ste:

Aparte de que hay alg¨²n n¨²mero repetido, y de que todas las filas, todas las columnas y las dos diagonales suman 33, en este cuadrado m¨¢gico hay muchas m¨¢s combinaciones num¨¦ricas que suman esa cantidad. En la imagen pod¨¦is ver algunas de ellas, pero hay m¨¢s. Os animo a que las busqu¨¦is y nos lo cont¨¦is en los comentarios.

Volvamos a los cuadrados con n¨²meros distintos. ?Qu¨¦ os parece uno solamente con n¨²meros primos? Los hay, y con n¨²meros primos consecutivos. Aqu¨ª ten¨¦is uno que contiene todos los n¨²meros primos desde el 79 hasta el 439, cuya constante m¨¢gica (suma de filas, columnas y diagonales) es 2016:

En Magic Square with Sequential Prime Numbers pod¨¦is ver otros cuadrados m¨¢gicos de distintos tama?os que contienen n¨²meros primos consecutivos.

Hasta ahora, en todos los cuadrados m¨¢gicos que os he presentado la operaci¨®n que usamos es la suma. ?Podremos encontrar cuadrados m¨¢gicos relacionados con otra operaci¨®n? Pues s¨ª, hay cuadrados m¨¢gicos de productos. Es decir, cuadrados m¨¢gicos en los que todas las filas, todas las columnas y las dos diagonales dan el mismo resultado al multiplicar sus t¨¦rminos. De ellos trataba uno de los desaf¨ªos matem¨¢ticos que propuso El Pa¨ªs, en colaboraci¨®n con la RSME, en el a?o 2011. Aqu¨ª ten¨¦is, como ejemplo, un cuadrado m¨¢gico de productos de orden 3.

Pero los hay m¨¢s grandes, claro que los hay. Aqu¨ª ten¨¦is uno de orden 8 que cumple que todas sus filas, todas sus columnas y las dos diagonales tienen como producto el n¨²mero 2058068231856000:

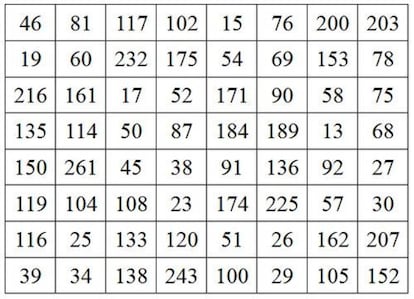
Magn¨ªfico, ?verdad? Bien, probad ahora a sumar sus filas. Correcto, todas suman 840. ?Y cu¨¢nto suman sus columnas? Pues s¨ª, 840. ?Y sus diagonales? Efectivamente, 840. Estamos ante un cuadrado num¨¦rico de orden 8 que es m¨¢gico para sumas y tambi¨¦n para productos. Maravilloso.

Estos cuadrados que son m¨¢gicos para sumas y productos no son los ¨²nicos que rebosan magia para dos operaciones. Echad un ojo a este cuadrado:

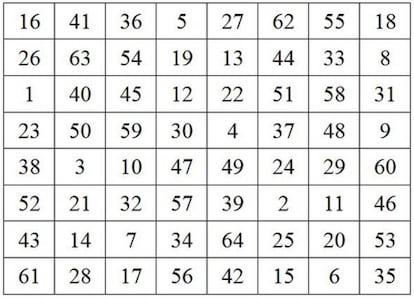
Sus filas, sus columnas y sus diagonales suman 260. Ahora, colocad en cada casilla el cuadrado de cada n¨²mero y sumad ahora filas, columnas y diagonales. Correcto, todas suman 11180. Esto significa que estamos ante un cuadrado m¨¢gico que nos da otro cuadrado m¨¢gico al elevar todos sus t¨¦rminos a 2.

?Pens¨¢is que ya se ha acabado? Pues no, a¨²n hay m¨¢s. Echad un ojo a este cuadrado, creado porBenjamin Franklin:

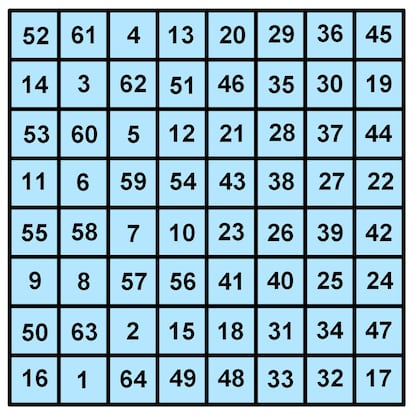
Si sum¨¢is las filas y las columnas, el resultado es 260, pero las diagonales suman otro n¨²mero. Pues tampoco es tan relevante como para citarlo aqu¨ª, ?verdad? Bien, sumad las esquinas. Da 130, la mitad de 260. Sumad los cuatro n¨²meros centrales, y tambi¨¦n da 130. Ahora tomad cualquier cuadrado de cuatro n¨²meros, el que quer¨¢is. Sumad sus elementos. ?Resultado? S¨ª, 130. Y una m¨¢s (posiblemente no la ¨²nica). Si sumamos los cuatro elementos de la diagonal ascendente 50-8-7-54 y al resultado le sumamos lo que da la suma de los cuatro de elementos de la correspondiente diagonal descendente, 43-26-25-47, el resultado es 260. Bien, pues esto funciona en todos los casos, tanto si empezamos con ascendente y seguimos con descendente como si lo hacemos al contrario. Sencillamente genial.

Vamos ahora con uno m¨¢s grande, de orden 13. Concretamente ¨¦ste:

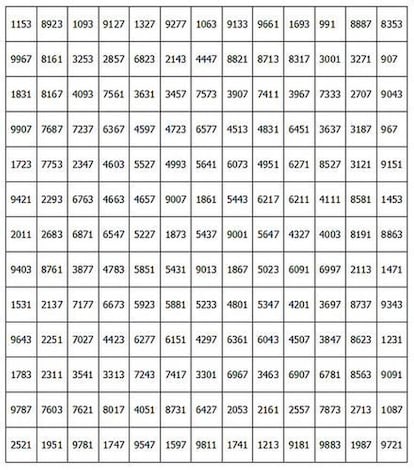
Su constante m¨¢gica es 70681. Tomad ahora el cuadrado de orden 3 central. Sumad filas, columnas y diagonales¡­Correcto, tambi¨¦n es un cuadrado m¨¢gico. Chul¨ªsimo, ?a que s¨ª? Bien, tomad ahora el de orden 5 central¡­tambi¨¦n es un cuadrado m¨¢gico. Y el de orden 7, y el de orden 9, y tambi¨¦n el de orden 11. Incre¨ªble¡­

¡­y lo es a¨²n m¨¢s si sabemos que la constante m¨¢gica de cada uno de ellos difiere en 10874 respecto de la del anterior. Es decir, la del de orden 11 es 70681-10874=59807; la del de orden 9 es 59807-10874=48933; la del de orden 7 es 48933-10874=38059; la del cuadrado de orden 5 es 38059-10874=27185; y la del de orden 3 es 27185-10874=16311. Aut¨¦nticamente asombroso.

Hemos visto cuadrados m¨¢gicos con n¨²meros primos, algunos que mezclan distintas operaciones y otros con algunas propiedades realmente interesantes y curiosas, pero todos est¨¢n relacionados directamente con n¨²meros. ?Con qu¨¦ pod¨ªan estarlo si no? Pues con la geometr¨ªa. Tambi¨¦n hay cuadrados m¨¢gicos con figuras geom¨¦tricas, llamados cuadrados geom¨¢gicos, como ¨¦stos:

En Geomagic Squares ten¨¦is muchos m¨¢s. Echadle un ojo, merece la pena.

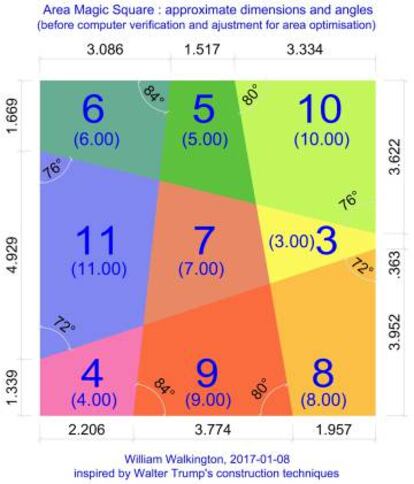
Para finalizar, os traigo el ¨²ltimo tipo de cuadrado m¨¢gico del que he tenido conocimiento: el cuadrado de ¨¢reas m¨¢gicas. En ¨¦l, cada regi¨®n tiene de ¨¢rea el n¨²mero que incluye, y el resultado da un cuadrado m¨¢gico habitual (filas, columnas y diagonales suman lo mismo). Aqu¨ª ten¨¦is un ejemplo para que lo ve¨¢is mejor.

Una preciosa manera de relacionar los cuadrados m¨¢gicos num¨¦ricos con la geometr¨ªa sobre la que pod¨¦is leer m¨¢s en Area Magic Squares and Tori of Order-3.

Como hab¨¦is podido ver, el mundo de los cuadrados m¨¢gicos posee multitud de variantes, tanto num¨¦ricas como geom¨¦tricas, y en este art¨ªculo he intentado mostraros algunas de ellas. ?Algunas? S¨ª, porque eso es lo mejor de todo: a¨²n hay mucho m¨¢s en lo que se refiere a cuadrados m¨¢gicos: los hay alfanum¨¦ricos (como el que nos mostraba Jos¨¦ Luis Carlavilla en este otro desaf¨ªo), los hay reversibles (como el que nos ense?an aqu¨ª en Futility Closet) y los hay tambi¨¦n creados a partir de fechas, que pueden dar juego utiliz¨¢ndolos con fechas de cumplea?os (como el que nos muestra Pedro Alegr¨ªa en este pdf). Y mucho, mucho mucho m¨¢s.

Por cierto, este art¨ªculo de Pedro Alegr¨ªa que acabo de enlazar (muy recomendable) contiene otro cuadrado m¨¢gico que quiero destacar. Antes de que lo ve¨¢is, os cuento c¨®mo construirlo. Tomad la fracci¨®n 1/19, realizad la divisi¨®n y quedaos con el per¨ªodo del n¨²mero decimal resultante. Ahora haced lo mismo con 2/19, con 3/19, y as¨ª hasta 18/19. Colocad todos esos per¨ªodos por filas en ese orden y obtendr¨¦is un cuadrado m¨¢gico de constante m¨¢gica 81. Bell¨ªsimo, ?verdad? Pues no es el ¨²nico. Seg¨²n nos comenta Pedro, tambi¨¦n puede hacerse de manera similar con la parte peri¨®dica de 1/383.

Y, ya s¨ª, concluyo este art¨ªculo divulgativo sobre el universo de los cuadrados m¨¢gicos con un v¨ªdeo dedicado al, posiblemente, m¨¢s importante divulgador de las matem¨¢ticas de la historia: Martin Gardner. Disfrutad: