Lord Kelvin, Pek¨ªn 2008 y un mon¨®logo de humor

Las abejas tienen habilidades matem¨¢ticas. Esto ya lo destac¨® Pappus de Alejandr¨ªa en el siglo IV cuando analiz¨® la forma en la que estos insectos construyen sus panales.

Adem¨¢s de por construir las celdas con un ¨¢ngulo final ¨®ptimo, la forma hexagonal de las celdas no parece ser ni mucho menos casual, ya que el hex¨¢gono regular es el pol¨ªgono que, a igual ¨¢rea, tiene menor per¨ªmetro, por lo que es el mejor para rellenar, o?teselar, un plano con pol¨ªgonos (es decir, para construir panales ¨®ptimos). Fue precisamente Pappus quien conjetur¨® este resultado, pero no lo demostr¨®.

Y as¨ª se mantuvo la cosa, sin demostraci¨®n, hasta 1999, a?o en el que Thomas Hales demostr¨® la veracidad de la conocida como conjetura del panal en su trabajo The Honeycomb Conjecture, cerrando as¨ª el c¨ªrculo: efectivamente, entre todos los pol¨ªgonos (sean convexos o no convexos) el hex¨¢gono regular es el pol¨ªgono m¨¢s eficiente para rellenar un plano.

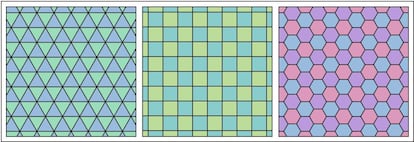
A partir de esto, surge de manera natural el hecho de preguntarse qu¨¦ ocurre en tres dimensiones. La pregunta, en este caso, ser¨ªa la siguiente: ?cu¨¢l es el poliedro que, a igual volumen, tiene menor ¨¢rea? O dicho de otra forma: ?cu¨¢l es el poliedro m¨¢s eficiente para rellenar el espacio tridimensional con ¨¦l?

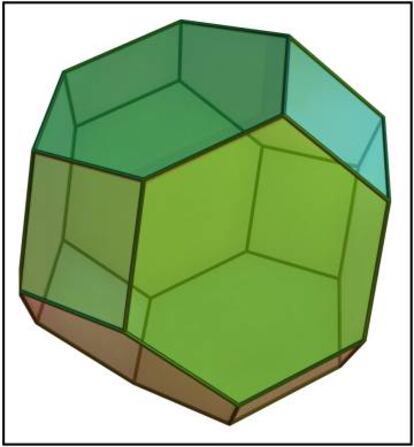
A finales del siglo XIX, Lord Kelvin conjetur¨® que ser¨ªa el octaedro truncado.

El propio William Thomson (que era el verdadero nombre de Lord Kelvin) estableci¨® esta conjetura en su trabajo On the division of space with minimum partitional area (que pod¨¦is descargar en pdf). Esto es lo que motiv¨® que este problema se denominara, a partir de ese momento, conjetura de Kelvin. En la siguiente imagen pod¨¦is ver c¨®mo quedar¨ªa un rellenado del espacio tridimensional con estos preciosos poliedros, los octaedros truncados:

Pero, como ocurri¨® en el caso anterior con Pappus, Lord Kelvin no pudo demostrar que el octaedro truncado era el poliedro m¨¢s eficiente entre todos los poliedros que son capaces de rellenar el espacio tridimensional. Era el mejor resultado conocido, pero no se sab¨ªa si era el m¨¢s eficiente.

El problema se mantuvo as¨ª hasta finales del siglo XX. En 1994, Denis Weaire y Robert Phelan publican el trabajo A counter-example to Kelvin¡¯s conjecture on minimal surfaces. En ¨¦l, como indica su propio t¨ªtulo, Weaire y Phelan presentan un contraejemplo a la conjetura de Kelvin dando un poliedro que es m¨¢s eficiente que el octaedro truncado a la hora de rellenar el espacio con ¨¦l. Dicho poliedro, conocido actualmente como estructura de Weaire-Phelan (s¨ª, un nombre muy original e imaginativo¡­), est¨¢ formado por dos dodecaedros irregulares con caras pentagonales y seis tetradecaedros con dos caras hexagonales y doce caras pentagonales y, seg¨²n el trabajo de Weaire y Phelan, es un 0¡¯3% m¨¢s eficiente que el octaedro truncado. Aqu¨ª ten¨¦is una imagen de esta estructura:

Bonita, ?verdad? Bonita y aparentemente complicada de montar. Quien est¨¦ interesado en montarla puede visitar este enlace de CutOutFoldUp, donde podr¨¢ encontrar distintas plantillas y los pasos necesarios para montar la estructura de Weaire-Phelan. Por cierto, esta web contiene much¨ªsimas plantillas e informaci¨®n para construir en papel una gran cantidad de figuras. Muy recomendable para los amantes de estas construcciones.

?Podr¨ªa tener esto alguna aplicaci¨®n pr¨¢ctica? Pues s¨ª, la tiene: construcciones. En los Juegos Ol¨ªmpicos de Pek¨ªn en 2008 pudimos ver una construcci¨®n basada en esta estructura: el Beijing National Aquatics Center:

Bien, entonces problema resuelto, ?verdad? Pues no. Weaire y Phelan encontraron una estructura m¨¢s eficiente que el poliedro de Kelvin, pero no demostraron que fuera la m¨¢s eficiente. Es decir, es m¨¢s eficiente que el octaedro truncado pero no se sabe si es la mejor posible, por lo que podr¨ªa encontrarse una estructura poli¨¦drica m¨¢s eficiente que la de Weaire-Phelan. O tambi¨¦n podr¨ªa demostrarse que, efectivamente, s¨ª que es la mejor posible. A d¨ªa de hoy seguimos sin saberlo, pero esperamos vivir lo suficiente como para poder contarlo.

Quien recuerde el t¨ªtulo de este art¨ªculo se estar¨¢ preguntado qu¨¦ tiene que ver un mon¨®logo de humor con todo esto. Pues lo explico ahora mismo. FameLab es un certamen de mon¨®logos cient¨ªficos cuyo objetivo es explicar conceptos de ciencia, tecnolog¨ªa o ingenier¨ªa mediante mon¨®logos de tres minutos. En 2013 se celebr¨® la primera edici¨®n de FameLab Espa?a, y el ganador fue el matem¨¢tico Eduardo S¨¢enz de Cabez¨®n (quien, dicho sea de paso, actualmente mantiene Derivando, un muy recomendable canal de YouTube en el que publica v¨ªdeos sobre matem¨¢ticas). El mon¨®logo con el que gan¨® se titulaba Un teorema es para siempre, y en ¨¦l hablaba sobre este tema de la conjetura del panal y la conjetura de Kelvin.

Creo que la mejor forma de terminar este art¨ªculo es, precisamente, disfrutar del mon¨®logo ganador de Eduardo. Aqu¨ª lo ten¨¦is: