El n¨²mero e y la prueba del carbono 14

El n¨²mero Pi, por todos conocido, aparece en multitud de f¨®rmulas e igualdades, como la identidad de Euler, y est¨¢ relacionado con una buena cantidad de situaciones reales (por ejemplo, aparece en el c¨¢lculo de longitudes, ¨¢reas y vol¨²menes de muchas figuras). Pero no es el ¨²nico n¨²mero curioso que aparece de manera recurrente relacionado con fen¨®menos de nuestro d¨ªa a d¨ªa.

Otro caso parecido al de Pi es el del n¨²mero e (que, por cierto, tambi¨¦n aparece en la identidad de Euler). Aunque las formas que conocemos para definirlo pueden parecer extra?as, la realidad es que aparece en muchas situaciones conocidas por todos, por lo que su utilidad pr¨¢ctica queda fuera de toda duda. Hoy vamos a hablar de una de ellas: la prueba del carbono 14, o dataci¨®n por radiocarbono, que fue desarrollada por Willard Libby a finales de los a?os 40 del siglo pasado.

Todos hemos o¨ªdo hablar sobre esta prueba, y sabemos que nos ayuda a datar restos (calcular cu¨¢ntos a?os tienen), aunque no tengamos muy claro c¨®mo funciona y por qu¨¦ es fiable. Vamos a intentar dar unas ideas sobre esta t¨¦cnica (sin entrar en demasiados detalles) para intentar aclarar esos puntos, deteni¨¦ndonos un poco m¨¢s en la parte matem¨¢tica.

El Carbono 14 es un is¨®topo radiactivo (inestable) del Carbono, que tiene otros dos is¨®topos, Carbono 12 y Carbono 13, que s¨ª son estables. Este is¨®topo Carbono 14 se genera espont¨¢neamente en la atm¨®sfera y, por otro lado, desaparece en parte por desintegraci¨®n radiactiva. Estos dos procesos est¨¢n equilibrados, por lo que dan como resultado que la cantidad de Carbono 14 permanece constante en, por decirlo de alguna forma, nuestro mundo.

Los seres vivos asimilan Carbono 14 a trav¨¦s de las plantas (que lo asimilan por fotos¨ªntesis), pero dejan de asimilarlo cuando mueren, momento en el que ese Carbono 14 comienza a desaparecer del ser vivo por desintegraci¨®n. Por tanto, si vemos qu¨¦ cantidad de Carbono 14 queda en una muestra y comparamos dicha cantidad con la que tiene una muestra viva, podemos ir hacia atr¨¢s y calcular su edad.

Para ello, todav¨ªa nos faltan algunas cosas. Una de ellas es saber la rapidez con la que se desintegra el Carbono 14. Bien, pues sobre esto sabemos que la velocidad de desintegraci¨®n de materia radiactiva a lo largo del tiempo es proporcional a la cantidad de dicha materia radiactiva. Esto lo sabemos gracias a los estudios de Ernest Rutherford y Frederick Soddy a principios del siglo XX.

Por otro lado, tambi¨¦n sabemos que el per¨ªodo de semidesintegraci¨®n o semivida del Carbono 14 es de 5730 a?os. Esto significa que, dada una muestra inicial a estudio, despu¨¦s de 5730 a?os se habr¨¢ desintegrado la mitad del Carbono 14 que conten¨ªa dicha muestra en un principio.

Si llamamos y a la cantidad de Carbono 14 de nuestra muestra, y tenemos en cuenta que esta cantidad depende del tiempo, tenemos que y es una funci¨®n de t: y(t). Sabiendo que la velocidad corresponde con la derivada, que ser¨ªa y¡¯(t), y teniendo en cuenta que la velocidad es proporcional a la cantidad, se tiene que la relaci¨®n que tenemos entre ellas es la siguiente:

y¡¯(t)= ¨C K ¡¤ y(t)

La constante de proporcionalidad K>0 se llama constante de desintegraci¨®n radiactiva, y el signo ¨C aparece porque la cantidad va disminuyendo al desintegrarse.

Esta relaci¨®n es una ecuaci¨®n diferencial, que en este caso es sencilla de resolver (es de?variables separables) teniendo en cuenta que y¡¯(t) es la derivada de y(t) respecto del tiempo t. Aqu¨ª os dejo la resoluci¨®n de la misma:

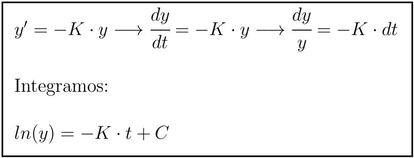
Ahora despejamos y(t) utilizando que la funci¨®n inversa del logaritmo neperiano es la exponencial. Obtenemos, despu¨¦s de unos c¨¢lculos (relativamente) sencillos, que la expresi¨®n de la cantidad de Carbono 14 es la siguiente:

??Apareci¨® el n¨²mero e!!

Nos quedan constantes por calcular A y K. Para ello, necesitamos un par de datos. Normalmente tendremos la cantidad inicial de Carbono 14 por comparaci¨®n con una muestra viva (cantidad a tiempo 0):

y(0)=y₀

y tambi¨¦n disponemos de la semivida de la que habl¨¢bamos antes, que en este caso es T=5730 a?os.

Con todo esto, ya podemos calcular las constantes. Es sencillo ver, utilizando la condici¨®n que nos da la cantidad inicial, que A=y₀. Por otro lado, usaremos el dato de la semivida (es decir, que y(T)=y₀/2) para calcular K y as¨ª obtener la soluci¨®n final de la ecuaci¨®n diferencial:

Ya lo tenemos todo. Ahora, dada una muestra muerta, tendr¨ªamos que comparar la cantidad de Carbono 14 que contiene con la cantidad que hay en una muestra viva para saber cu¨¢nto se ha desintegrado, y aplicar la expresi¨®n anterior para ver cu¨¢nto hace que dicha muestra muri¨®.

Veamos un ejemplo. Supongamos que encontramos una muestra f¨®sil (muerta) y al compararla con una muestra viva obtenemos que solamente queda un 15% de Carbono 14. Si la muestra viva tiene una cantidad y₀ de Carbono 14, la muerta tendr¨¢ 0¡¯15 ¡¤ y₀. Calculemos ahora la edad del f¨®sil:

Usando ahora que T=5730, la edad de dicho f¨®sil ser¨¢, aproximadamente, de unos 15682 a?os.

Es interesante comentar que esta prueba, por la corta semivida del Carbono 14, sirve para datar muestras de, como mucho, unos 50000 a?os. Y tambi¨¦n conviene comentar que se toma como fecha base para tirar hacia atr¨¢s el a?o 1950, ya que desde ese a?o ha habido fluctuaciones significativas en las cantidades de esta sustancia por las pruebas nucleares realizadas desde ese momento. Seguro que hay muchos detalles t¨¦cnicos relacionados con todo esto que me he dejado sin comentar (y, posiblemente, alguna que otra imprecisi¨®n qu¨ªmica), pero el objetivo del art¨ªculo era dar una visi¨®n matem¨¢tica del asunto.

Como ¨²ltimo dato sobre la dataci¨®n por radiocarbono, comentar que fue decisiva para desmentir que la conocida como S¨¢bana Santa fuera en realidad un sudario de la ¨¦poca en la que, supuestamente, vivi¨® Jesucristo, ya que mediante este proceso se estableci¨® que dicho sudario proven¨ªa de, aproximadamente, el siglo XIII.

Como pod¨¦is ver, hay otros n¨²meros extra?os, adem¨¢s de Pi, que tienen importancia e inter¨¦s en la vida diaria. Este n¨²mero e es, posiblemente, el m¨¢ximo exponente de todos ellos, ya que tanto ¨¦l como su funci¨®n asociada, la exponencial, aparecen en muchos procesos naturales. El conocimiento de este n¨²mero y esta funci¨®n y de sus propiedades nos puede ayudar en muchas situaciones, como la descrita en este art¨ªculo. Si conoc¨¦is alguna m¨¢s, estaremos muy agradecidos si nos las cont¨¢is en los comentarios.