El mayor n¨²mero primo conocido

Es posible que el n¨²mero 1398269 no os diga nada especial, pero la realidad es que podemos decir que representa el comienzo de una nueva era dentro de la b¨²squeda de n¨²meros primos. Era noviembre de 1996 y se encontraba un n¨²mero primo de 420921 cifras que a la postre result¨® ser especial, y no solamente por la enorme cantidad de d¨ªgitos que posee. Pero antes de hablar de ese momento, centremos hist¨®ricamente el asunto.

La b¨²squeda de n¨²meros primos, sobre todo desde que Euclides demuestra que existen infinitos, ha sido un tema que ha apasionado a much¨ªsimos, y muy buenos, matem¨¢ticos a lo largo de la historia. M¨¢s concretamente, la b¨²squeda de una f¨®rmula que genere siempre n¨²meros primos distintos ha quitado el sue?o a, posiblemente, todos los matem¨¢ticos que se han acercado en sus estudios a este tema.

Una de las ¨¦pocas en las que esta b¨²squeda tuvo uno de sus momentos ¨¢lgidos fue el siglo XVII. La correspondencia de Pierre de Fermat con otros matem¨¢ticos marca el comienzo de la teor¨ªa de n¨²meros como rama de las matem¨¢ticas, y los n¨²meros primos son unos de sus principales protagonistas. Fermat da una f¨®rmula que, seg¨²n dice, genera siempre n¨²meros primos (todos ellos distintos), pero se equivoca, como demostr¨® Euler m¨¢s adelante.

Fermat no fue el ¨²nico. En esa misma ¨¦poca, Mar¨ªn Mersenne, un sacerdote, matem¨¢tico y fil¨®sofo franc¨¦s, introduce una expresi¨®n aparentemente simple que a la larga ha resultado interesant¨ªsima en lo que se refiere a encontrar n¨²meros primos realmente grandes.

Mersenne estudia los n¨²meros de la forma 2ⁿ-1 en su obra Cogitata Physica-Mathematica, de 1644, y da algunos datos sobre ellos. Mersenne sabe que esos n¨²meros, que suelen llamarse M_n, no son siempre primos, pero la sensaci¨®n es que esta f¨®rmula acaba dando n¨²meros primos para una cantidad nada despreciable de valores de n. Adem¨¢s, Mersenne da una lista de n¨²meros primos calculados con esa f¨®rmula hasta n=257. Es cierto que se equivoca (da alguno como primo y omite otros que s¨ª lo son), pero todo este estudio es el comienzo de la b¨²squeda de n¨²meros primos de Mersenne.

Los siete primeros n¨²meros primos de Mersenne, que eran los que se conoc¨ªan hasta la ¨¦poca del propio Mersene, son los que aparecen en la siguiente tabla:

De aqu¨ª en adelante esta lista fue aumentando, pero a un ritmo algo lento. En 1771, Leonhard Euler encuentra el octavo primo de Mersenne, que corresponde con el exponente n=31:

M₃₁ = 2³¹ ¨C 1 = 2147483647

Exceptuando los de exponente muy peque?o, que eran f¨¢ciles de comprobar por dar resultados bastante bajos, los primos de Mersenne conocidos hasta ese momento se hab¨ªan calculado mediante comprobaci¨®n directa: se probaba un n¨²mero primo en el exponente, se calculaba el n¨²mero y despu¨¦s se realizaban divisiones entre los n¨²meros primos inferiores a ¨¦l para ver si era divisible entre alguno de ellos. Este m¨¦todo puede ser ¨²til cuando el n¨²mero a comprobar es relativamente bajo, pero cuando ese n¨²mero es grande el tiempo dedicado a la comprobaci¨®n ser¨ªa tan grande que el m¨¦todo pasa a ser in¨²til en la pr¨¢ctica.

Por cierto, acabamos de decir que se probaba con n¨²meros primos en el exponente. ?Por qu¨¦ no se probaba con n¨²mero compuestos? Por ejemplo, ?no podr¨ªamos probar con n=16 ¨® n=28? Pues s¨ª, podr¨ªamos, pero ser¨ªa totalmente in¨²til porque se sabe que, si n es compuesto, el n¨²mero 2ⁿ ¨C 1 tambi¨¦n es compuesto (y, por tanto, no es primo). ?Alguien sabr¨ªa demostrarlo? Pod¨¦is hacerlo en los comentarios.

La b¨²squeda de n¨²meros primos de Mersenne avanz¨® con los estudios de ?douard Lucas, que desarroll¨® un m¨¦todo para comprobar si un n¨²mero de la forma 2^p ¨C 1 era primo (mucho m¨¢s eficaz que el de comprobaci¨®n directa). Con este m¨¦todo, Lucas demostr¨®, a finales del siglo XIX, que 2¹²⁷ ¨C 1 es un n¨²mero primo. Hasta mediados de los a?os 50 del siglo XX, ¨¦ste era el mayor n¨²mero primo conocido, y adem¨¢s es el n¨²mero primo m¨¢s grande que se ha encontrado sin ayuda de ordenadores.

Y aqu¨ª est¨¢ la clave del asunto: el ordenador. El desarrollo de la inform¨¢tica y el m¨¦todo de Lucas, que fue mejorado por Derrick Henry Lehmer sobre 1930, son los causantes de que hayamos conseguido encontrar n¨²meros primos de Mersenne muchos m¨¢s grandes.

Este m¨¦todo, llamado actualmente test de Lucas-Lehmer, consiste en lo siguiente. Supongamos que queremos comprobar si cierto n¨²mero M_p = 2^p ¨C 1 es primo. Pues, para ello, seguimos el siguiente proceso:

(Pod¨¦is ver una demostraci¨®n de este resultado en este enlace de The Prime Pages, web en la que pod¨¦is encontrar gran cantidad de informaci¨®n sobre n¨²meros primos.)

Aunque s_p-2 es un n¨²mero mayor que M_p, el test da el resultado mucho m¨¢s r¨¢pido que si hacemos la comprobaci¨®n directa (por ejemplo, para utilizar este m¨¦todo no necesitamos conocer todos los n¨²meros primos menores que el n¨²mero que estamos comprobando).

Sin usar este test, se conoc¨ªan los 12 primeros n¨²meros de Mersenne. En 1952 se comienza a utilizar el test de Lucas-Lehmer en un ordenador¡­y en ese a?o se encuentran cinco m¨¢s (del 13 al 17 de la lista). A partir de aqu¨ª, la lista contin¨²a creciendo hasta el que ocupa el n¨²mero 34 en la lista de primos de Mersenne, que ya tiene la nada despreciable cantidad de 378632 d¨ªgitos¡­

¡­y llegamos al a?o 1996 que cit¨¢bamos al principio del art¨ªculo. A principios de ese a?o, George Woltman crea GIMPS (Great Internet Mersenne Prime Search). La idea de esta iniciativa es ofrecer un software, que utiliza el test de Lucas-Lehmer, para que quien quiera pueda descargarlo y as¨ª contribuya a la b¨²squeda de primos de Mersenne. Cuando se encuentra un n¨²mero de la forma 2^p ¨C 1 que el test da como primo, se realizan comprobaciones para corroborarlo. Si esas comprobaciones dan resultados positivos, se declara como primo ese n¨²mero.

Con este software, y la ayuda de muchos internautas, GIMPS ha conseguido 15 nuevos n¨²meros primos de Mersenne, con lo que la lista actual de estos n¨²meros contiene 49 primos. Adem¨¢s, se encargan de comprobar que no nos hemos dejado ninguno por el camino (recordad que no necesitamos conocer los primos anteriores a nuestro n¨²mero-objetivo, por lo que, por poner un ejemplo, podr¨ªa salirnos antes el que ocupar¨ªa el n¨²mero 60 que el ocupar¨ªa en n¨²mero 59 en la lista ordenada).

El primero que encontraron, a finales de 1996, fue el que cit¨¢bamos en el primer p¨¢rrafo del art¨ªculo: M_1398269. A d¨ªa de hoy, GIMPS ha comprobado que la lista es exhaustiva hasta el n¨²mero 45, pero todav¨ªa no se sabe si desde ah¨ª hasta el mayor conocido hoy nos hemos dejado alguno sin encontrar. Est¨¢n en ello, y cuando todos los c¨¢lculos est¨¦n realizados lo anunciar¨¢n en su p¨¢gina web, donde tambi¨¦n pod¨¦is ver, entre otras cosas, la lista completa de primos de Mersenne.

Volvamos ahora al t¨ªtulo del art¨ªculo: El mayor n¨²mero primo conocido. ?Cu¨¢l es? Pues el n¨²mero siguiente:

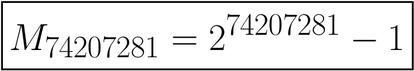
S¨ª, el exponente es 74207281. Es decir, que si quisi¨¦ramos calcularlo a mano tendr¨ªamos que multiplicar 2 por s¨ª mismo esa cantidad de veces y despu¨¦s restar 1 al resultado. Casi nada.

Este n¨²mero primo tiene la descomunal cifra de 22338618 d¨ªgitos. S¨ª, m¨¢s de 22 millones de d¨ªgitos. Es un n¨²mero enorme, enorme, enorme, mucho m¨¢s grande de lo que una persona pueda imaginar. Para intentar hacernos una lejan¨ªsima idea sobre la magnitud de este n¨²mero, pensad en lo siguiente:

Imaginad que ten¨¦is un mill¨®n de euros (o pensad en ese mill¨®n si lo ten¨¦is en realidad). Es mucho dinero, much¨ªsimo, ?verdad? Bien, pues un mill¨®n es un n¨²mero que tiene solamente 7 cifras.

Y una ¨²ltima curiosidad sobre los primos de Mersenne. Est¨¢ demostrado que cada n¨²mero primo de Mersenne genera un n¨²mero perfecto (que es un n¨²mero que es igual a la suma de todos sus divisores excepto ¨¦l mismo). M¨¢s concretamente, si M_p es primo, entonces el producto 2^{p ¨C 1} ¡¤ M_p es un n¨²mero perfecto. Otro detalle que hace que estos n¨²meros primos de Mersenne sean maravillosos.

Habl¨¢bamos unos p¨¢rrafos m¨¢s arriba sobre la b¨²squeda de una f¨®rmula que genere siempre n¨²meros primos. En la actualidad no se ha encontrado ninguna f¨®rmula de ese tipo, y ni siquiera sabemos si existe tal f¨®rmula. Lo que s¨ª tenemos son expresiones particulares, como la de los n¨²meros de Mersenne, que generan n¨²meros primos para ciertos exponentes. Y no es la ¨²nica, existen otras expresiones que tambi¨¦n generan n¨²meros primos de manera relativamente habitual y plataformas que ya las est¨¢n estudiando utilizando su propio software. Os animo a que busqu¨¦is informaci¨®n sobre ellas y, si pod¨¦is, os un¨¢is a las mismas. Qui¨¦n sabe, quiz¨¢s alguna de las personas que est¨¢ leyendo este art¨ªculo sea el descubridor de, por ejemplo, el primer n¨²mero primo de m¨¢s de 100 millones de d¨ªgitos.