Una paradoja de pelotas

Seg¨²n el Diccionario de la RAE, el t¨¦rmino ¡°paradoja¡±, en su segunda acepci¨®n, se define de la siguiente forma:

Paradoja: Hecho o expresi¨®n aparentemente contrarios a la l¨®gica.

A nuestro alrededor, en nuestra vida diaria, podemos encontrar muchas cuestiones que podr¨ªan encuadrarse dentro del mundo de las paradojas, pero dejemos ¨¦stas aparte y centr¨¦monos en el tema del que trata este blog: las matem¨¢ticas.

En matem¨¢ticas no es dif¨ªcil encontrarse con paradojas de todo tipo (como, por ejemplo, la paradoja de Bertrand de la que hablamos hace un tiempo): las hay relacionadas con la l¨®gica en s¨ª misma, con la teor¨ªa de conjuntos, con la probabilidad, con el c¨¢lculo, con la geometr¨ªa¡­

Relacionada con esta ¨²ltima rama de las matem¨¢ticas est¨¢ la paradoja que vamos a analizar en este art¨ªculo. Su nombre, paradoja de la banda esf¨¦rica, quiz¨¢s no nos muestre demasiado sobre su contenido, pero s¨ª que m¨¢s o menos nos induce a pensar que la cosa va ¡°de pelotas¡±. Veamos de qu¨¦ trata el asunto.

Supongamos que tenemos una esfera peque?a, digamos del tama?o de una pelota de ping pong. Tomamos un hilo y la rodeamos completamente por su ecuador, nos quedamos con el trocito que hemos usado para rodear y le a?adimos un metro m¨¢s de hilo. Despu¨¦s, colocamos el hilo obtenido (el que sali¨® al rodear junto con el metro a?adido) alrededor del ecuador. Como quedar¨¢ espacio entre nuestro hilo y el ecuador, intentamos que dicho espacio sea el mismo para todos los puntos (es decir, que el hilo y el ecuador est¨¦n a la misma distancia en todos los puntos). Hecho esto, nos preguntamos lo siguiente: ?el hueco que queda entre hilo y pelota es muy grande o muy peque?o? ?Podr¨ªamos pasar a trav¨¦s de ¨¦l un bol¨ªgrafo BIC con capucha (de, en total, unos 15 cm de altura)?

Tomemos ahora una esfera mayor, por ejemplo una del tama?o del t¨ªpico mapamundi que muchos hemos tenido en casa en alg¨²n momento, y hagamos lo mismo: hilo alrededor del ecuador, a?adimos un metro de hilo al trozo obtenido al rodear y colocamos el hilo resultante alrededor del ecuador dejando, en todos los puntos, el mismo espacio. ?C¨®mo ser¨¢ ahora el hueco que hemos obtenido? ?Podremos ahora hacer pasar el bol¨ªgrafo por ¨¦l?

Y ahora a lo grande, por qu¨¦ no: tomemos una esfera del tama?o de nuestro planeta y repitamos la operaci¨®n: rodeamos el ecuador con un hilo, despu¨¦s lo aumentamos un metro y a continuaci¨®n lo colocamos a distancia uniforme del ecuador. ?Qu¨¦ tama?o tendr¨¢ este hueco en relaci¨®n con los anteriores? ?Pasar¨¢ ahora nuestro boli por dicho hueco?

Como pod¨¦is ver, los tama?os de las esferas elegidas son distintos, bastante distintos (de una pelota de ping pong a una esfera como La Tierra va un buen trecho¡­). Lo m¨¢s habitual, al menos lo que m¨¢s ha ocurrido cuando he planteado esta cuesti¨®n a alguien, es que nuestra intuici¨®n nos diga que el boli pasar¨¢ f¨¢cilmente por el hueco que queda con la pelota de ping pong, que le cueste m¨¢s con el que deja el mapamundi (o que incluso no pase) y que ni de broma quepa por el hueco obtenido con una esfera como nuestro planeta.

Bien, pues la soluci¨®n es la siguiente: los tres huecos son exactamente iguales. En cada punto del ecuador de las tres esferas, la distancia entre dicho punto y el que le corresponder¨ªa en el hilo alargado es exactamente la misma. ?Os ha chocado el resultado? ?Quer¨¦is ver c¨®mo calcular dicha distancia con unas matem¨¢ticas muy simples? Seguid leyendo.

En general, lo que ocurre es que el hueco que queda entre hilo y ecuador es independiente del radio de la esfera inicial, por lo que tomemos la esfera que tomemos obtendremos que el hueco tiene siempre el mismo tama?o. Vamos a tomar una esfera de radio R cualquiera, medido en metros, y hagamos c¨¢lculos.

Calculamos la longitud del ecuador con la f¨®rmula para calcular la longitud de una circunferencia:

L = 2 ¡¤ ¦Ð ¡¤ R

?sa ser¨ªa la longitud del hilo con el que rodeamos la esfera. Ahora a?adimos un metro a ese hilo, obteniendo la longitud de la circunferencia que quedar¨ªa separada de nuestra esfera:

L¡¯ = 2 ¡¤ ¦Ð ¡¤ R + 1

Pero esta longitud se puede calcular de otra manera. Pensad que la nueva circunferencia tendr¨¢ como radio el de la inicial, R, m¨¢s un poco m¨¢s, digamos r, que de hecho es la distancia que queremos calcular. Como el radio de la misma ser¨¢ entonces R + r, su longitud puede calcularse as¨ª:

L¡¯ = 2 ¡¤ ¦Ð ¡¤ (R + r)

Vamos a calcular la distancia que buscamos, r, igualando las dos expresiones de L¡¯ y despejando:

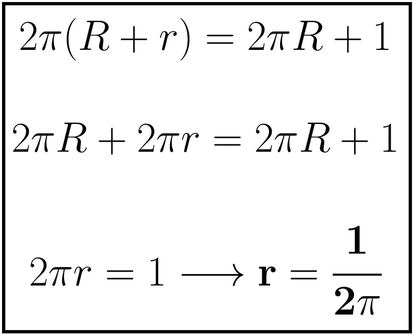
Hemos obtenido que r (la distancia buscada) es, efectivamente, independiente del radio de la esfera inicial y, adem¨¢s, que su valor es 1 dividido entre 2¦Ð. Ese valor es 0¡¯159154¡­, con lo que, teniendo en cuenta que hemos considerado que r viene expresado en metros, tenemos que la distancia en cada punto entre hilo y ecuador es de casi 16 cm. Por tanto, en los tres ejemplos mostrados m¨¢s arriba (y con cualquier otra esfera, sea del tama?o que sea), nuestro boli BIC pasar¨¢ sin demasiada dificultad por el hueco obtenido.

?Os ha sorprendido el resultado? Si pensasteis que los huecos eran de tama?os distintos no os preocup¨¦is. Tiene cierto sentido pensar eso, ya que si relacionamos el hueco con el tama?o de la esfera, tenemos que cuando m¨¢s peque?a es dicha esfera m¨¢s grande se ver¨ªa ese hueco en relaci¨®n con ella. Pero, como hab¨¦is visto, las matem¨¢ticas nos aseguran que da igual si tomamos inicialmente una canica, un bal¨®n de baloncesto o una esfera un mill¨®n de veces mayor que nuestro Sol, en todos los casos el hueco ser¨ªa el mismo: 16 cm. Curioso, ?verdad?

?Hab¨¦is pensado que los huecos iban siendo cada vez m¨¢s peque?os? ?O vuestra intuici¨®n os dijo otra cosa? Contadnos en los comentarios qu¨¦ os ha sugerido el problema, seguro que es interesante ver lo que ha pensado cada uno de vosotros. Y, ya de paso, si nos habl¨¢is de alguna otra paradoja que sea digna de comentar por aqu¨ª mucho mejor.