C¨®mo calcular ¨¢reas contando puntitos

Os voy a proponer un problema. Imaginad que queremos calcular el ¨¢rea de este pol¨ªgono irregular:

En principio, la cosa parece complicada: no tenemos datos sobre longitudes ni alg¨²n tipo de referencia para comenzar a pensar. Podr¨ªamos triangular el pol¨ªgono (recordad que todo pol¨ªgono es triangulable), hacer mediciones a mano y despu¨¦s utilizar la f¨®rmula para calcular el ¨¢rea de un tri¨¢ngulo, pero corremos el riesgo de cometer alg¨²n error al medir (aunque sea peque?o), lo que provocar¨ªa que el resultado que obtendr¨ªamos para el ¨¢rea no ser¨ªa exacto.

Vamos a buscar alguna referencia antes de seguir pensando. Tomamos unos ejes coordenados y colocamos el v¨¦rtice inferior izquierdo en el origen, en el punto (0,0):

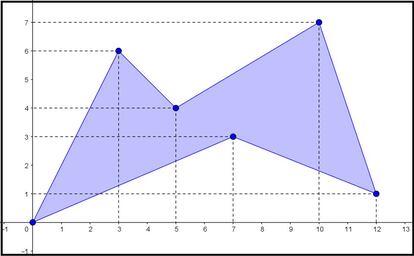
Como pod¨¦is ver en la imagen, se da la curiosa circunstancia de que el resto de v¨¦rtices de nuestro pol¨ªgono tambi¨¦n est¨¢n situados en puntos cuyas dos coordenadas son n¨²meros enteros. Pues para este caso disponemos de una manera muy sencilla, e inesperada, de calcular el ¨¢rea del pol¨ªgono. Veamos c¨®mo podemos hacerlo.

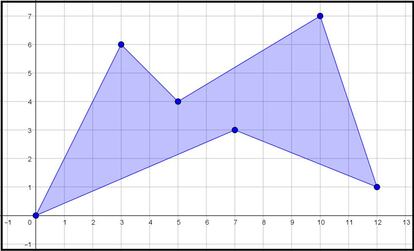
Coloquemos ahora una cuadr¨ªcula mediante la cual podamos ver con facilidad todos los puntos con coordenadas enteras que hay en la zona donde tenemos dibujado nuestro pol¨ªgono:

Marcamos ahora en la cuadr¨ªcula todos los puntos que quedan en el interior del pol¨ªgono (en rojo en la siguiente imagen) y todos los que quedan exactamente sobre alguno de los lados del mismo, incluso los v¨¦rtices (en azul en la imagen). En este caso, nos quedar¨ªa algo as¨ª:

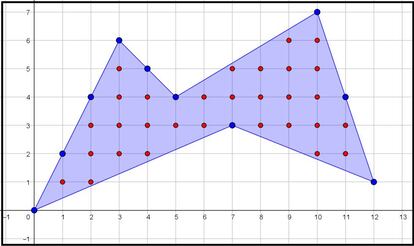
Contemos ahora cu¨¢ntos hay de cada tipo. Tenemos 30 puntos en el interior (en rojo) y 10 puntos en el borde del pol¨ªgono (en azul). Ahora dividimos la cantidad de puntos del borde entre 2, le sumamos la cantidad de puntos del interior y restamos 1 al resultado. En nuestro ejemplo, obtenemos 30 + 5 ¨C 1 = 34. Bien, pues el ¨¢rea de nuestro pol¨ªgono es exactamente 34.

Aqu¨ª ten¨¦is una imagen en la que podemos ver el valor del ¨¢rea que nos da el programa GeoGebra (debajo del pol¨ªgono) y el valor que nos dan las operaciones que acabamos de describir:

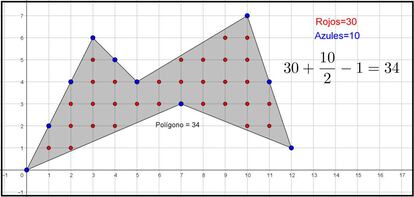
Esto significa que para calcular el ¨¢rea de un pol¨ªgono cuyos v¨¦rtices tienen todos coordenadas enteras simplemente hay que contar puntos interiores y puntos del borde y realizar las operaciones citadas. Curioso y inesperado, ?verdad?

Este resultado se conoce como teorema de Pick, debido a que fue el matem¨¢tico austriaco Georg Alexander Pick quien lo demostr¨® en el a?o 1899. Aqu¨ª ten¨¦is el enunciado m¨¢s o menos formal del teorema:

Dada una cuadr¨ªcula en la que cada intersecci¨®n corresponde con un punto del plano, supongamos que tenemos un pol¨ªgono P sin agujeros cuyos v¨¦rtices est¨¢n todos situados en intersecciones de la cuadr¨ªcula. Si I es el n¨²mero de intersecciones que quedan en el interior del pol¨ªgono y B el n¨²mero de intersecciones que quedan sobre alg¨²n lado del mismo, se tiene que el ¨¢rea de dicho pol¨ªgono puede calcularse mediante la siguiente f¨®rmula:

A = I + B/2 ¨C 1

Aunque demostrar este teorema no es excesivamente dif¨ªcil, creo que excede las pretensiones de este art¨ªculo, por lo que he decidido no incluir ninguna demostraci¨®n del mismo. De todas formas, no es dif¨ªcil encontrarla por internet. Si alguien encuentra alguna demostraci¨®n de este teorema (se conocen varias esencialmente distintas) que vea con inter¨¦s para compartirla con nosotros, le agradeceremos que nos hable de ella en los comentarios.

Aunque la restricci¨®n de que todos los v¨¦rtices tengan coordenadas enteras puede rebajar un poco la euforia matem¨¢tica que deber¨ªa invadir nuestras mentes al conocer este teorema, no se puede negar su inter¨¦s y, sobre todo, lo inesperado de la relaci¨®n entre el ¨¢rea de un pol¨ªgono y cantidades de puntitos. Seguro que, si no lo conoc¨ªais, os ha sorprendido.

Y un ¨²ltimo apunte: en tres dimensiones no tenemos un resultado que sea directamente equivalente al teorema de Pick, ya que hay poliedros cuyos v¨¦rtices tienen todos coordenadas enteras para los que su volumen no coincide con el resultado que nos dar¨ªa el teorema de Pick. Una l¨¢stima.