Tetraedrizando, que es gerundio

Se sabe desde hace mucho tiempo que todo pol¨ªgono es triangulable. La triangulaci¨®n de pol¨ªgonos es un proceso muy ¨²til en diversas situaciones, y el hecho de que todo pol¨ªgono se pueda triangular facilita mucho las cosas a la hora de, por ejemplo, calcular ¨¢reas de figuras irregulares.

Lo anterior significa que todo pol¨ªgono, figura bidimensional limitada por segmentos, puede descomponerse en figuras cuya forma es el pol¨ªgono con el menor n¨²mero de lados posibles: el tri¨¢ngulo. Pero, posiblemente, lo que muchos no os hab¨¦is preguntado es si se puede hacer lo mismo en tres dimensiones, es decir, si cualquier poliedro (figura tridimensional limitada por pol¨ªgonos, llamadas caras) puede descomponerse en distintas partes cuya forma sea el poliedro con el menor n¨²mero de caras posible: el tetraedro. La pregunta ser¨ªa algo as¨ª: ?todo poliedro es tetraedrizable?

Antes de nada, vamos a comentar qu¨¦ es exactamente triangular un pol¨ªgono. Una triangulaci¨®n de un pol¨ªgono es una divisi¨®n de dicho pol¨ªgono en tri¨¢ngulos que cumple que la uni¨®n de todos los tri¨¢ngulos da el pol¨ªgono inicial, que todos los v¨¦rtices de los tri¨¢ngulos son v¨¦rtices del pol¨ªgono inicial (es decir, no a?adimos ni quitamos v¨¦rtices) y que todos los tri¨¢ngulos comparten entre s¨ª, como mucho, un v¨¦rtice o un lado.

Con estas condiciones, todo pol¨ªgono es triangulable. Por ver un ejemplo, os dejo aqu¨ª una triangulaci¨®n de un pol¨ªgono de once lados:

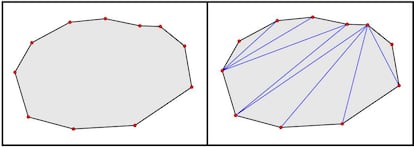
Como hemos comentado, triangular un pol¨ªgono puede ser muy interesante para, por ejemplo, calcular ¨¢reas de figuras poligonales extra?as. La idea ser¨ªa triangular esa superficie bidimensional y aprovechar que el ¨¢rea de un tri¨¢ngulo es muy f¨¢cil de calcular (base por altura dividido entre 2). Calculamos las ¨¢reas de todos los tri¨¢ngulos, sumamos y ya tenemos el ¨¢rea de la figura inicial.

Visto esto, la cuesti¨®n ahora es preguntarse qu¨¦ ocurre en tres dimensiones. Ya hemos visto por aqu¨ª que, en ocasiones, el paso a tres dimensiones es complicado, como pasaba en el problema de los besos de las esferas. Veamos qu¨¦ ocurre en este caso.

Como dec¨ªamos antes, la idea es ver si puede dividirse cualquier poliedro en tetraedros, que es el poliedro con el menor n¨²mero posible de caras. Vamos, nos preguntamos lo siguiente: ?todo poliedro es tetraedrizable? Se entiende, con unas condiciones equivalentes al caso de la triangulaci¨®n: que la uni¨®n de los tetraedros sea el poliedro inicial, que todos los v¨¦rtices de los tetraedros sean v¨¦rtices del inicial (es decir, que no haya que a?adir ni quitar v¨¦rtices) y que cada dos tetraedros compartan, como mucho, un v¨¦rtice, una arista o una cara.

En lo que se refiere a triangular un pol¨ªgono, se puede hacer tanto si el pol¨ªgono es convexo como si no lo es. Con los poliedros no ocurre eso: todo poliedro convexo es tetraedrizable, pero no todo poliedro no convexo es tetraedrizable. Este descubrimiento es relativamente reciente, concretamente de 1911. En ese a?o, N. J. Lennes construy¨® un poliedro no convexo que no era tetraedrizable. Algo despu¨¦s, en 1928, Eric Sch?nhardt dio un ejemplo m¨¢s sencillo simplificando la construcci¨®n anterior, quedando el que ahora se conoce como poliedro de Sch?nhardt:

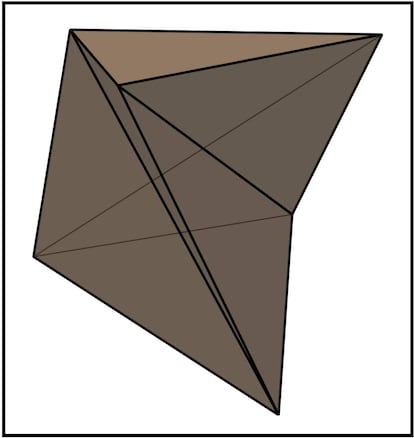
Extra?o, ?verdad? Es posible que con esa imagen uno no sea capaz de construirse una buena idea mental de esta figura. Por ello, os dejo este v¨ªdeo en el que se ve en movimiento a este curioso poliedro:

Para finalizar, es interesante comentar que ¨¦ste no es el ¨²nico caso de poliedro no tetraedrizable. Despu¨¦s del de Sch?nhardt, se descubrieron m¨¢s figuras poli¨¦dricas que no pueden dividirse en tetraedros con las condiciones descritas. Algunos ejemplos son el poliedro de Thurston y el poliedro de Chazelle. En The Geometry Junkyard ten¨¦is m¨¢s informaci¨®n sobre ellos.

En matem¨¢ticas, el hecho de que al pasar de dos a tres dimensiones cambien caracter¨ªsticas o se pierdan propiedades es, posiblemente, m¨¢s habitual de lo que uno podr¨ªa esperar. Hay muchos m¨¢s ejemplos de situaciones en las que ocurren cosas parecidas a la que ocurre con las tetraedrizaciones. Seguro que vosotros conoc¨¦is m¨¢s casos, y si es as¨ª estaremos muy agradecidos si los compart¨ªs con nosotros en los comentarios.