El principio de Cavalieri

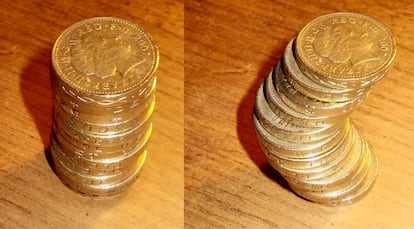
Nos pregunt¨¢bamos la semana pasada c¨®mo pod¨ªamos hallar un valor aproximado de ¦Ð mediante alg¨²n proceso aleatorio en la l¨ªnea del m¨¦todo de Montecarlo. He aqu¨ª uno bastante sencillo: trazamos con tiza en el suelo (o con un l¨¢piz en una hoja de papel) un c¨ªrculo inscrito en un cuadrado; no importa que la figura no sea geom¨¦tricamente perfecta, pues vamos a conformarnos con un valor aproximado, y puesto que ya conocemos el valor de ¦Ð, en realidad lo que vamos a comprobar es la eficacia del m¨¦todo. Si llamamos r al radio de la circunferencia (no hace falta que lo midamos), el ¨¢rea del cuadrado ser¨¢ (2r)2 = 4r2, y el ¨¢rea del c¨ªrculo, ¦Ðr2. Si ahora lanzamos un buen n¨²mero de objetos peque?os (guijarros, garbanzos, monedas, etc.) sobre la figura, por ejemplo 50, y 39 quedan dentro del c¨ªrculo, partiendo del supuesto de que el n¨²mero de objetos es proporcional al ¨¢rea podemos establecer la igualdad 39/50 = ¦Ð/4, de donde ¦Ð = 3,12. Si el resultado se aleja mucho del valor real de ¦Ð, o no hemos lanzado suficientes objetos, o el lanzamiento no ha sido aleatorio.

Mediante una simulaci¨®n por ordenador, se puede hacer que aparezcan puntos al azar (con un generador de n¨²meros aleatorios) en una figura como la descrita, y es f¨¢cil ver que a medida que aumenta el n¨²mero de puntos el resultado se va aproximando al valor real de ¦Ð (ver los comentarios 10 y 34 de la semana pasada).

Los indivisibles de Cavalieri

Algunos de nuestros ¡°usuarios destacados¡± se enzarzaron en un interesante debate sobre probabilidades (un tema inagotable en el que las falacias y las paradojas proliferan por doquier), y en alg¨²n momento se aludi¨® al teorema de Fubini. Es un teorema relativo a las integrales, un campo en el que no nos adentraremos, pues requiere conocimientos que van m¨¢s all¨¢ de las matem¨¢ticas b¨¢sicas. Pero en el siglo XVII otro matem¨¢tico italiano, Bonaventura Cavalieri, formul¨® un principio que podr¨ªa considerarse un caso particular del teorema de Fubini, y que es anterior a las integrales y al c¨¢lculo infinitesimal propiamente dicho.

Siguiendo a Arqu¨ªmedes, Cavalieri introduce el concepto de ¡°indivisibles¡± (claro antecedente de los infinitesimales), secciones muy finas que permiten, por adici¨®n, calcular vol¨²menes cuyas f¨®rmulas no se pueden determinar por m¨¦todos convencionales. En esencia, el principio de Cavalieri afirma que si dos cuerpos tienen la misma altura e igual ¨¢rea en sus secciones planas realizadas al mismo nivel, tienen igual volumen. Este principio se puede ilustrar con dos pilas de monedas iguales: es evidente que tendr¨¢n el mismo volumen aunque una de las pilas forme un cilindro perfecto y en la otra las monedas (que representan los ¡°indivisibles¡± de Cavalieri) est¨¦n desplazadas.

Sabemos que el volumen del cilindro es ¦Ðr2h (¨¢rea de la base por la altura) y el del cono ¦Ðr2h/3 (un tercio del ¨¢rea de la base por la altura). ?C¨®mo podemos, a partir de aqu¨ª y aplicando el principio de Cavalieri, hallar la f¨®rmula del volumen de la esfera?

Carlo Frabetti es escritor y matem¨¢tico, miembro de la Academia de Ciencias de Nueva York. Ha publicado m¨¢s de 50 obras de divulgaci¨®n cient¨ªfica para adultos, ni?os y j¨®venes, entre ellos Maldita f¨ªsica, Malditas matem¨¢ticas o El gran juego. Fue guionista de La bola de cristal.