Peinando cabezas con matem¨¢ticas

?Qui¨¦n no tiene un remolino en la cabeza que, por mucho tiempo que le dedique, no puede peinar? Vale, los calvos no, pero (no se me molesten, por favor) dej¨¦moslos fuera del tema a estudio por un momento.

Todos, en alguna ocasi¨®n, hemos tenido que luchar con un remolino de pelo que no hemos podido domar, ya sea en nuestra propia cabeza o en la cabeza de alguien cuyo cabello hemos intentado domesticar. Pues la existencia de dichos remolinos, aunque pueda parecer incre¨ªble, tiene explicaci¨®n matem¨¢tica. Vamos a ello.

Pong¨¢monos en situaci¨®n. Vamos a imaginar una pelota (una esfera tridimensional) llena de pelo, con un pelo en cada punto de la superficie de la misma. Al ¡°peinar¡± dicha pelota lo que hacemos es, b¨¢sicamente, colocar cada pelo de forma tangente a la propia pelota. Algo as¨ª como lo que puede verse en esta imagen (las flechas ser¨ªan los pelos):

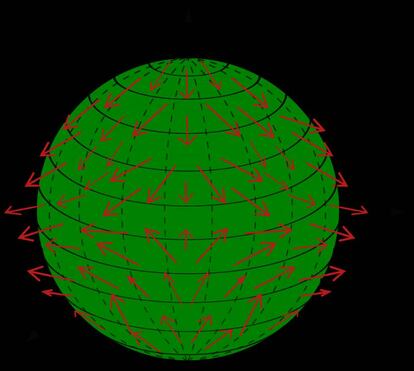
Esta disposici¨®n de vectores tangentes a cada punto de la superficie de la pelota se llama campo de vectores tangentes a la esfera. Como nuestro objetivo es ¡°peinar¡± la pelota completa, necesitar¨ªamos que en todos los puntos el vector tangente (el pelo) fuera como una de esas flechitas. O, dicho de manera informal, que ¡°el pelo saliera hacia afuera¡±. En t¨¦rminos de vectores, necesitar¨ªamos que el vector tangente a cada punto de la superficie de la esfera fuera distinto del vector cero (as¨ª tendr¨ªamos flechita tangente)

Bien, pues el teorema de la bola peluda dice que todo campo de vectores tangentes sobre la esfera tiene al menos un cero. Es decir, peinemos como peinemos (usemos el campo de vectores tangentes que usemos) siempre habr¨¢ al menos un punto en el que nos toparemos con un remolino (un vector tangente cero).

M¨¢s formalmente, llamando a la esfera tridimensional como S² (que es como suele denotarse), podr¨ªamos enunciar el teorema de la bola peluda de la siguiente forma:

"Sea F : S² ¡ú R³ un campo continuo de vectores tangentes sobre S². Entonces existe al menos un punto p₀ de S² tal que F(p₀)=0."

De hecho, este teorema es v¨¢lido para toda ¡°esfera¡± Sⁿ, con n un n¨²mero par mayor o igual que 2. Es decir, si pudi¨¦ramos tener una ¡°pelotita¡± S⁴ (objeto que ¡°vive¡± es un espacio de cinco dimensiones), tampoco podr¨ªamos ¡°peinarla¡± completamente. Ahora, para Sⁿ, con n impar, s¨ª que se puede. Por ejemplo, es sencillo verlo para S¹, que es una ¡°esfera¡± en dos dimensiones (esto es, una circunferencia).

Por cierto, este teorema fue conjeturado por primera vez por Henri Poincar¨¦ a finales del siglo XIX y demostrado por Luitzen Egbertus Jan Brouwer en 1912.

Si llevamos esto a nuestra cabeza, y suponi¨¦ndola esf¨¦rica (no lo es, pero nos sirve) y con un pelo en cada punto de su superficie (de acuerdo, en realidad no es as¨ª, pero para el caso nos vale), nunca podremos peinarla de forma perfecta, siempre nos encontraremos alg¨²n remolino que, irremediablemente, no podremos ¡°arreglar¡±.

Como en muchas otras ocasiones, uno podr¨ªa pensar que el teorema de la bola peluda es otro resultado matem¨¢tico m¨¢s sin importancia y sin aplicaciones pr¨¢cticas. El propio teorema (como todos) tiene ya inter¨¦s e importancia matem¨¢tica, pero adem¨¢s nos ayuda a explicar un fen¨®meno meteorol¨®gico.

Tomemos el planeta Tierra como una esfera (vale, ¨¦sta tampoco es una esfera perfecta, pero nos vuelve a servir) y el viento en cada punto de la misma como campo de vectores tangentes. Por el teorema de la bola peluda, habr¨¢ al menos un punto de la superficie de nuestro planeta en que el vector tangente ser¨¢ el vector cero. Ese vector cero es una especie de huequecito, alrededor del cual tendr¨ªamos el remolino. ?Veis por d¨®nde voy? Un hueco, un remolino alrededor¡­Mirad la imagen:

??Un cicl¨®n!! El teorema de la bola peluda es la explicaci¨®n matem¨¢tica de por qu¨¦ en todo momento hay al menos un cicl¨®n en la superficie de la Tierra. Y, dependiendo de c¨®mo sople el viento (es decir, dependiendo del campo de vectores tangentes que tengamos), en un cierto instante podr¨ªa haber m¨¢s de uno (el teorema dice ¡°al menos uno¡±, pero no nos da ni un n¨²mero exacto ni un n¨²mero m¨¢ximo).

Como curiosidad final, imaginemos que en vez que querer peinar una ¡°bola peluda¡±, lo que queremos peinar es una ¡°rosquilla peluda¡±. Pues, en este caso, s¨ª podremos: es posible peinar a la perfecci¨®n una rosquilla peluda. Teniendo en cuenta que en matem¨¢ticas a las rosquillas se las llama toros, se tiene lo siguiente:

"Es posible definir sobre un toro un campo de vectores tangentes que no tiene ning¨²n cero."

?Quer¨¦is verlo? Aqu¨ª ten¨¦is un ejemplo de peinado del toro:

?Se os ocurren m¨¢s figuras tridimensionales que puedan ser peinadas de esta manera? Cont¨¢dnoslo en los comentarios.