El Juego del Drago

Estamos ya casi en plena Navidad, ¨¦poca en la que muchos grupos de familiares y amigos aprovechan para reunirse despu¨¦s de, en ocasiones, mucho tiempo sin compartir momentos juntos. En estas fechas son t¨ªpicas las comilonas y, despu¨¦s de ellas, las tardes y noches de conversaci¨®n y diversi¨®n con esos seres queridos.

Hoy os quiero presentar un juego que, aunque hace ya a?os que se cre¨®, no es muy conocido y puede servir para pasar un buen rato con otra persona. Se trata del Juego del Drago, tambi¨¦n conocido como Brotes, inventado por los matem¨¢ticos John Horton Conway y Michael Stewart Patterson en la d¨¦cada de los 60 del pasado siglo XX.

Seguro que la gran mayor¨ªa de vosotros ha jugado al juego de los puntitos, o de los cuadritos (en mi casa lo llam¨¢bamos los ceros). Este juego para dos jugadores consiste en dibujar una cuadr¨ªcula de puntitos o circulitos (por eso lo de los ceros) del tama?o que queramos en la que despu¨¦s ambos jugadores, con turnos alternativos, dibujan l¨ªneas rectas (horizontales o verticales) que unan dos puntos consecutivos. Cuando un jugador dibuja una l¨ªnea que completa un cuadrado, lo marca como suyo (colore¨¢ndolo con su color, poni¨¦ndole la inicial de su nombre¡­) y dibuja una nueva l¨ªnea. Gana el que m¨¢s cuadrados haya conseguido marcar como propios.

Bien, pues el juego de hoy tambi¨¦n va de unir puntitos con l¨ªneas, pero de una forma un poco distinta. Vamos a explicar sus reglas y su mec¨¢nica.

El Juego del Drago, tambi¨¦n para dos jugadores, comienza con una cierta cantidad de puntos dispuestos de la forma que queramos, cuantos m¨¢s puntos m¨¢s largo ser¨¢ el juego y mayor complejidad tendr¨¢. Esos puntos se llaman brotes, y la mec¨¢nica del juego es que, de manera alternativa, cada jugador una con una l¨ªnea, llamada rama (no necesariamente recta, vale una curva), dos de esos brotes o un brote consigo mismo y, despu¨¦s, a?ada un nuevo brote encima de la l¨ªnea que acaba de dibujar.

Por ejemplo, comenzando con tres brotes podr¨ªamos unir dos como muestra la figura siguiente, y a?adir entonces un nuevo brote sobre dicha l¨ªnea (el de color verde):

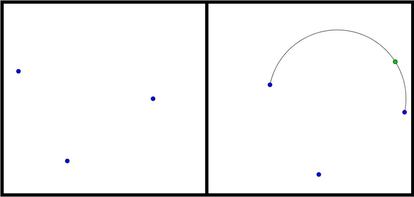
Pero no podemos a?adir l¨ªneas a nuestro antojo, sino que debemos seguir tres reglas:

1.- La rama (que, como hemos dicho, no tiene por qu¨¦ ser recta) no puede cortarse a s¨ª misma ni tampoco a otra rama que ya estuviera dibujada.

2.- Una rama no puede pasar por otros brotes que no sean los dos que queremos unir.

3.- No pueden salir m¨¢s de tres ramas de ning¨²n brote.

Cuando de un brote sale exactamente tres ramas, se dice que el brote est¨¢ muerto, y por tanto ya no podr¨¢ usarse para dibujar una nueva rama.

Llegar¨¢ un momento en el que ya no se puedan dibujar m¨¢s l¨ªneas, ya sea porque todos los brotes han muerto, porque al dibujar una l¨ªnea superemos las tres ramas en un cierto brote, porque las ¨²nicas ramas que podamos a?adir corten a alguna que ya est¨¢ dibujada¡­En ese caso, en la versi¨®n habitual del juego, gana el jugador que haya a?adido la ¨²ltima rama.

Para que la cosa se entienda un poco mejor, os dejo una posible partida del Juego del Drago comenzando con tres brotes. En cada imagen pod¨¦is ver una jugada en la que se dibuja una rama y se a?ade un nuevo brote en ella (el punto verde):

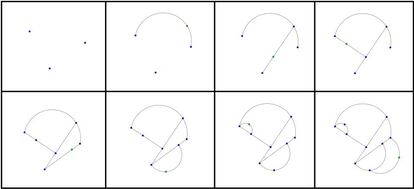
Y ya no se pueden hacer m¨¢s movimientos, ya que los ¨²nicos brotes que todav¨ªa sobreviven son los que aparecen en rojo en la siguiente imagen pero no se pueden unir sin cortar a una rama que ya est¨¦ dibujada (incumplir¨ªamos la primera regla):

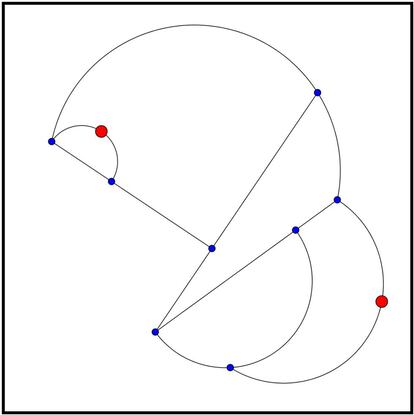
Tampoco podemos a?adir una rama que una uno de esos dos brotes consigo mismo, ya que entonces tendr¨ªamos un brote del que salen cuatro ramas, incumpliendo as¨ª la tercera regla.

Como suele ser habitual en estos juegos, se ha estudiado matem¨¢ticamente el juego del drago en lo que a finalizaci¨®n y estrategias se refiere (trat¨¢ndose de un juego creado por dos matem¨¢ticas, ser¨ªa un delito no hacerlo en este caso). La primera cuesti¨®n que es interesante plantearse es si todas las partidas terminar¨¢n. Teniendo en cuenta que en cada movimiento aumenta el n¨²mero de brotes, podr¨ªa ser que alguna partida pudiera alargarse indefinidamente¡­

¡­pero eso es imposible en este juego. De hecho, est¨¢ demostrado que, si se comienza con N brotes, el n¨²mero de turnos es, como mucho, 3N-1. Es decir, todas las partidas del juego del drago terminan. Por dar otro dato, tambi¨¦n se sabe que, como m¨ªnimo, cada partida tendr¨¢ 2N turnos.

Y, por otro lado, est¨¢ la cuesti¨®n de las posibles estrategias que pueden seguir los jugadores con el objetivo de ganar una partida. La cuesti¨®n es que, al ser un juego que acaba en un n¨²mero finito de pasos y en el cual no se puede empatar, el juego del drago tiene estrategia ganadora para alguno de los dos jugadores. Otra cosa es encontrar dicha estrategia¡­

La cuesti¨®n es que, actualmente, se sabe para qu¨¦ jugador hay estrategia ganadora en unos cuantos casos, que dependen del n¨²mero inicial de brotes. Por ejemplo, con 2 brotes hay estrategia para que gane el segundo jugador; para 3, 4, y 5 brotes iniciales la hay para que sea el primer jugador el que resulte ganador; para 6, 7 y 8 brotes el segundo jugador tiene estrategia ganadora; para 9, 10 y 11 la tiene el primero¡­

?Veis alg¨²n patr¨®n? Parece que s¨ª, ?verdad? Tranquilos, no os emocion¨¦is todav¨ªa. Cierto es que parece que la posesi¨®n de estrategia ganadora sigue un patr¨®n en funci¨®n del n¨²mero inicial de brotes, pero, por desgracia, en la actualidad es solamente una conjetura. M¨¢s concretamente, es esta conjetura:

Hasta donde yo s¨¦, a d¨ªa de hoy se conoce (est¨¢ demostrado) para qu¨¦ jugador hay estrategia ganadora para todos los n¨²meros iniciales de brotes hasta 44, y tambi¨¦n para 46, 47 ¨® 53, y todos esos casos cuadran con la conjetura anterior. Pero todav¨ªa no se sabe si la conjetura resultar¨¢ ser cierta o si, por el contrario, alg¨²n valor del n¨²mero inicial de brotes incumplir¨¢ la misma.

Para finalizar, comentar que hay otras variantes del juego, por ejemplo la que da como perdedor (en vez de como ganador) al que dibuj¨® la ¨²ltima rama. Sobre la versi¨®n habitual, las otras versiones del juego y algunos estudios que se han realizado sobre el mismo ten¨¦is m¨¢s informaci¨®n en Computer Analysis of Sprouts y en Computer Analysis of Sprouts with nimbers.

?Conoc¨ªais este juego? Despu¨¦s de conocerlo, ?os hab¨¦is animado a echar alguna partida? Contadnos vuestra experiencia en los comentarios. Y si conoc¨¦is otros juegos sencillos de jugar y con inter¨¦s, como el juego del drago, no dud¨¦is en compartirlos con nosotros.