Desmontando (una vez m¨¢s) los absurdos sorteos por letra

Los vemos en muchos lugares, se suelen usar para determinar un orden de participaci¨®n o para elegir a los agraciados en un cierto sorteo. Estamos hablando de los sorteos por letra, y en lo que sigue vamos a intentar explicar una vez m¨¢s por qu¨¦ estos sorteos deber¨ªan dejar de hacerse por ser totalmente injustos.

Me he animado a escribir sobre esto cuando he visto que, de nuevo, el orden de participaci¨®n en la parte oral de las Oposiciones a Profesor de Ense?anza Secundaria en Castilla-La Mancha se ha vuelto a determinar eligiendo (se entiende que al azar) una letra del abecedario, concretamente la M (aqu¨ª ten¨¦is la resoluci¨®n). Quiz¨¢ en casos como este el orden no es tan importante (o s¨ª, vaya usted a saber), pero tambi¨¦n se usa este m¨¦todo para determinar los ganadores de las entradas a un espect¨¢culo, las familias cuyos hijos podr¨¢n ir a cierto colegio o guarder¨ªa o los agraciados con una vivienda. Casi nada.

La raz¨®n por la que estos sorteos deber¨ªan desaparecer es muy sencilla: los sorteos por letra no dan la misma probabilidad a todos los participantes, y por lo tanto no son sorteos justos. Se entiende que un sorteo debe ser justo en el sentido de que todos los participantes tengan la misma probabilidad de obtener el ¡°premio¡±, sea este cual sea, ?verdad? Pues en los sorteos con letra esto no es as¨ª, o al menos no es as¨ª en todos los casos.

En algunos casos, un sorteo as¨ª podr¨ªa ser justo, pero antes habr¨ªa que estudiar si todos los participantes tienen la misma probabilidad de ¡°ganar¡±, y os aseguro que esto no se hace nunca. Por tanto, encontrar al menos un caso en el que este tipo de sorteos no es justo deber¨ªa ser raz¨®n suficiente para que los sorteos por letra dejen de hacerse.

Vamos a poner un ejemplo en el que veremos claramente lo injusto de este tipo de sorteos, pero antes no est¨¢ de m¨¢s aclarar de qu¨¦ van estos sorteos por letra por si alguien no lo tiene claro.

Para explicarlo, voy a usar primero el ejemplo de las oposiciones. Imaginemos que 200 opositores llegan a la parte oral, que consiste en exponer algo (no nos hace falta especificar) ante un tribunal. Est¨¢ estipulado que el orden de actuaci¨®n de dichos opositores ser¨¢ alfab¨¦tico, pero el opositor que actuar¨¢ en primer lugar no se elige al azar, sino que se saca una letra al azar y la primera persona cuyo apellido comience con esa letra se convierte en el primero en exponer.

Podr¨ªa parecer que este sorteo es justo, pero no es as¨ª porque no todos los opositores tienen la misma probabilidad de ser elegidos en primer lugar. Como dec¨ªa antes, puede que en este caso no sea tan importante, pero imaginad que en vez del primer puesto al exponer lo que se sortea en un premio de 10.000 euros. ?Os gustar¨ªa saber desde antes del sorteo que no ten¨¦is ninguna probabilidad de ganarlo? Supongo que no.

Vamos ahora a ver un ejemplo concreto para que la cosa quede m¨¢s clara. Tomemos los apellidos de, por ejemplo, 16 matem¨¢ticos que ya han aparecido por El Aleph: Euler, Fermat, Bohr, Goodstein, Gauss, Banach, Ulam, Van Aubel, Conway, Cs¨¢sz¨¢r, Pick, Simson, Newton, Cantor, Jordan y Bolyai. Ahora, entre ellos, vamos a sortear un puesto como catedr¨¢tico de la universidad m¨¢s prestigiosa del mundo, y lo vamos a hacer mediante un sorteo por letra: metemos en una bolsa 27 bolitas con las 27 letras del abecedario, sacamos una y el primero cuyo apellido empiece por esa letra se lleva la c¨¢tedra. Si no hay nadie cuyo apellido comience con la letra que salga, pasamos a la letra siguiente del abecedario, y as¨ª sucesivamente.

Echando un vistazo por encima a los apellidos, podemos sacar interesantes conclusiones. Por ejemplo, Bohr y Bolyai se pueden olvidar del premio ya que no tienen ninguna posibilidad de salir elegidos. Repito, ninguna. Y no tienen ninguna porque Banach est¨¢ delante de ellos alfab¨¦ticamente, y aunque salga la B ellos no podr¨¢n recibir esa ansiada c¨¢tedra

Por otra parte, Fermat se la llevar¨ªa si sale la F, pero solamente en ese caso; sin embargo, Banach obtendr¨ªa el premio si sale la B... Y tambi¨¦n si sale la W, o la X, o la Y, o la Z o la A. Por tanto, Banach tiene muchas m¨¢s opciones que, por ejemplo, Fermat. ?Os parece justo?

Para calcular la probabilidad de cada uno de ellos, simplemente habr¨ªa que dividir el n¨²mero de casos favorables (el n¨²mero de letras con las que se gana) entre el n¨²mero de casos posible (27, las letras que se usan para el sorteo). Os dejo a continuaci¨®n una tabla con los porcentajes de victoria que tendr¨ªa cada uno de nuestros protagonistas en este sorteo por letra ficticio:

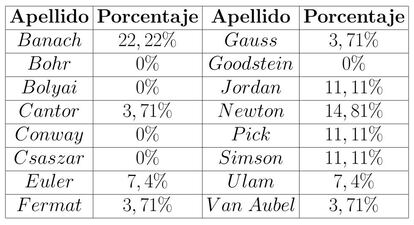
Como ya hab¨ªamos comentado, y como se puede ver en la tabla, no todos tienen la misma probabilidad de salir premiados, por lo que el sorteo es a todas luces injusto.

Imaginemos ahora que en vez de una c¨¢tedra se sortean dos. En este caso, algunos que antes no pod¨ªan ganar ahora s¨ª que tienen una probabilidad positiva de ello, pero sigue habiendo valores desiguales en las probabilidades y gente que sigue sin tener ninguna opci¨®n, como el pobre Janos Bolyai (que en el mejor de los casos, que salga la B, sigue teniendo por delante a Banach y a Bohr). Y da igual el n¨²mero de premios que demos, el sorteo sigue siendo injusto.

En algunos lugares razonan de la siguiente forma: ¡°vale, con una letra la cosa no es justa¡­Saquemos dos letras y asunto arreglado¡±. Nada de asunto arreglado, estamos en las mismas: el sorteo sigue siendo injusto. Volviendo a nuestro ejemplo anterior, Bohr se llevar¨ªa la c¨¢tedra si salieran BB, BC, BD, BE, BF,¡­, BO (15 casos), mientras que Fermat, por citar uno, se la llevar¨ªa si salen EV, EW, EX, EY, EZ, FA, FB, FC, FD o FE (10 casos)¡­?Y Bolyai seguir¨ªa teniendo probabilidad cero de ganar! As¨ª que lo dicho, sacar una letra m¨¢s no arregla nada¡­

¡­Ni dos letras m¨¢s, ni sacar del primer apellido y del segundo, ni del apellido de nuestro abuelo por parte de madre, ni del de nuestra t¨ªa la soltera que est¨¢ forrada. Mientras los apellidos de los participantes no sean equiprobables en relaci¨®n con las letras que sacamos, todos los sorteos por letra son injustos. Punto final.

Y por si todav¨ªa hay alguien que no se haya convencido de ello, vamos a tirar de pasta, de dineros, que as¨ª seguro que nos queda m¨¢s claro. Imaginad que en el pr¨®ximo sorteo de Loter¨ªa de Navidad meten la bola de 65535 siete veces, la del 87654 la dejan fuera del bombo y de los dem¨¢s n¨²meros meten una bola por cada uno. ?Comprar¨ªa alguien un boleto con el n¨²mero 87654? ?Comprar¨ªais alg¨²n otro que no fuera el 65535? ?Pagar¨ªais igual por un boleto de ese n¨²mero que por uno del, por ejemplo, 12345? Seguro que no, ya que en esta situaci¨®n no todos los n¨²meros tienen la misma probabilidad de salir. ?Ha quedado ahora m¨¢s claro? Espero que s¨ª.

Con lo f¨¢cil que es asignar un n¨²mero a cada uno de los participantes y sacar al azar uno de los n¨²meros asignados, no s¨¦ por qu¨¦ se sigue usando este m¨¦todo totalmente injusto. Y, relacionado con esto, dejo una pregunta para finalizar este art¨ªculo. Ah¨ª va:

Imaginemos que asignamos un n¨²mero a los, digamos, 100 participantes en un sorteo y que hay dos premios iguales, digamos de 1.000 euros cada uno. Procedemos de la siguiente forma:

Asignamos a los participantes los n¨²meros del 1 al 100 de forma aleatoria, y despu¨¦s, tambi¨¦n aleatoriamente, sacamos una bola y le damos el premio a quien tenga el n¨²mero de dicha bola y al que tenga el n¨²mero siguiente (si sale el 100, se le da al 100 y al 1). En este caso, ?tendr¨ªan todos la misma probabilidad de salir agraciados con 1.000 euros? ?O la forma correcta ser¨ªa sacar una bola, dar el premio, dejar dicha bola fuera de la bolsa y sacar otra bola para entregar el siguiente premio?

Contadnos lo que pens¨¢is sobre todo esto en los comentarios.