?Puede ser una p¨¦sima idea ir en coalici¨®n?

Llegamos al tercero y ¨²ltimo de los desaf¨ªos matem¨¢ticos que EL PA?S y la Real Sociedad Matem¨¢tica Espa?ola est¨¢n proponiendo con motivo del periodo electoral. Como los anteriores, lo presentan, Ang¨¦lica Benito Sualdea y Adolfo Quir¨®s Graci¨¢n, profesores de Matem¨¢ticas en la Universidad Aut¨®noma de Madrid.

El desaf¨ªo trata sobre la diferencia entre los resultados electorales que conseguir¨ªa una coalici¨®n y los que alcanzar¨ªan los partidos por separado. Los lectores pueden enviar sus respuestas hasta las 00.00 del lunes 20 de mayo (la medianoche del domingo al lunes, hora peninsular espa?ola) a problemamatematicas@gmail.com.

A continuaci¨®n, para aclarar dudas, a?adimos el enunciado del problema por escrito.

En Espa?a la mayor¨ªa de los procesos electorales se rigen por el m¨¦todo D'Hondt, cuyo funcionamiento explicamos en el desaf¨ªo anterior. Veamos qu¨¦ sucede, usando el m¨¦todo D'Hondt, si dos partidos deciden ir en coalici¨®n bajo la hip¨®tesis (no del todo realista) de que todos los votantes que fuesen a optar por uno de ellos votan a la coalici¨®n.

Puede ser que la coalici¨®n obtenga los mismos esca?os que habr¨ªan obtenido los partidos por separado. Por ejemplo, si hay que repartir 3 esca?os entre 3 partidos que han obtenido respectivamente 100, 100 y 70 votos, tenemos la siguiente tabla:

Como 70>50, D'Hondt asigna un esca?o a cada partido.

Si los dos partidos mayores van en coalici¨®n y suman los votos:

obtendr¨¢n 2 esca?os, pero no m¨¢s, porque 100>70 pero 66,6<70.

Tambi¨¦n puede ser que la coalici¨®n gane esca?os.Por ejemplo, si en una elecci¨®n como la que acabamos de explicar los votos fuesen 105, 105 y 60, la situaci¨®n ser¨ªa:

Por separado, cada partido obtiene un esca?o.

Pero ahora, si los dos partidos mayores suman sus votos tenemos:

y, como 70>60, la coalici¨®n se llevar¨ªan los 3 esca?os, quit¨¢ndole al partido C el que ganaba.

Lo que no puede pasar es que una coalici¨®n obtenga menos esca?os que los partidos por separado (insistimos, bajo la hip¨®tesis de que todos los votantes que fuesen a optar por uno de ellos votan a la coalici¨®n), y uno de los motivos para elegir el m¨¦todo D'Hondt cuando se celebraron las primeras elecciones democr¨¢ticas en 1977, un momento en el que Espa?a hab¨ªa lo que se conoc¨ªa como "sopa de letras de partidos", fue precisamente que incentiva las coaliciones.

Demostremos ahora que la coalici¨®n no pierde esca?os. Supongamos que el partido A ha obtenido u votos y n esca?os, y el B ha obtenido v votos y m esca?os.

Llamemos q al ¨²ltimo cociente que ha obtenido esca?o.

Tenemos entonces:

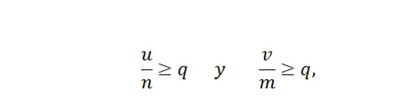
o, lo que es lo mismo

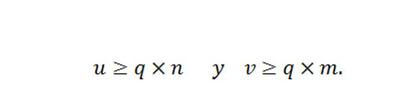
Sumando ambas desigualdades se tiene

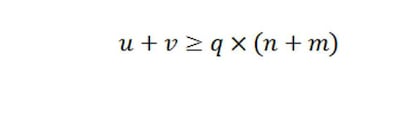
y, por tanto,

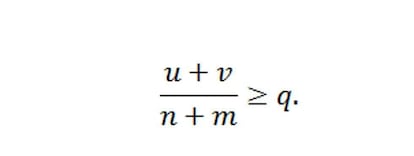
Esto muestra que, como q era el punto de corte para obtener esca?os, y los votos de los dem¨¢s partidos no han cambiado, una coalici¨®n de A y B que sumase todos los votos obtendr¨ªa al menos n+m esca?os antes de llegar al ¨²ltimo cociente q. Podr¨ªa obtener m¨¢s, como muestra el ejemplo anterior, pero no menos.

El desaf¨ªo que proponemos consiste en analizar qu¨¦ puede suceder con una coalici¨®n si, en lugar de D'Hondt utiliz¨¢semos otro m¨¦todo que se ha propuesto en alg¨²n momento para su uso en Espa?a: el de Sainte-Lagu?. Funciona de manera similar al de D'Hondt, pero dividiendo los votos s¨®lo entre 1, 3, 5, 7,¡­ (por eso se llama tambi¨¦n m¨¦todo de los divisores impares).

Los lectores tienen que decidir si, usando el m¨¦todo de Sainte-Lagu?, dos partidos que se presenten en coalici¨®n y que reciban los votos de todos los que habr¨ªan votado a cada uno de ellos, pueden obtener los mismos esca?os, ganar esca?os o perder esca?os con respecto a la suma de los que habr¨ªan logrado por separado.

Para cada una de las tres posibilidades hay que, como hemos hecho nosotros para D`Hondt, o bien dar un ejemplo en el que se produzca, o bien dar una demostraci¨®n de que no puede producirse.