Un flotador biplaza

Ya hay soluci¨®n para el vig¨¦simo sexto desaf¨ªo matem¨¢tico con el que EL PA?S celebra el centenario de la Real Sociedad Matem¨¢tica Espa?ola (ver el v¨ªdeo conmemorativo).

Mar¨ªa Pe Pereira, que es licenciada y doctora en Matem¨¢ticas por la Universidad Complutense de Madrid y actualmente disfruta de una beca posdoctoral de CajaMadrid en el Institut de Math¨¦matiques de Jussieu en Par¨ªs, propuso el problema (ver v¨ªdeo de la izquierda) y lo resuelve ahora (v¨ªdeo de la derecha): la respuesta es un flotador para 2 personas.

Para este desaf¨ªo se han recibido en el plazo marcado 318 respuestas, de las que el 81% son correctas. El ganador de una biblioteca matem¨¢tica como la que entrega cada semana EL PA?S ha sido en esta ocasi¨®n Miguel Rodr¨ªguez Guti¨¦rrez, de Madrid. Este domingo, en el quiosco, por 9,95 euros con el peri¨®dico, La poes¨ªa de los n¨²meros, de Antonio J. Dur¨¢n.

Recordemos el problema: consist¨ªa en saber qu¨¦ superficie se pod¨ªa obtener pegando -sin retorcer innecesariamente- los lados del mismo color de la figura dada, de tal manera que el sentido de las flechas coincidiera y pudiendo deformarla todo lo necesario sin romperla: se pod¨ªa estirar, contraer...

La respuesta correcta al desaf¨ªo es un flotador para 2 personas (doble toro o superficie orientable de g¨¦nero 2, en terminolog¨ªa matem¨¢tica), una de las superficies sin borde de la clasificaci¨®n que se daba.

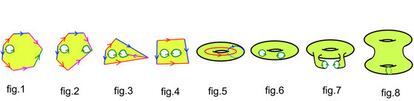
Veamos una soluci¨®n detallada bas¨¢ndonos en las figuras de arriba (ver ampliaci¨®n aqu¨ª). Empezamos fij¨¢ndonos en que tenemos que pegar los lados violetas. En la figura 2, solo pegamos dos v¨¦rtices, empujando el lado verde hacia el interior de la figura. En la figura 3, pegamos los lados violetas completos, estirando la figura hacia la derecha hasta hacerlos coincidir. En la figura 4, por comodidad, puesto que el pol¨ªgono resultante tiene cuatro lados, le damos forma cuadrada. As¨ª reconocemos m¨¢s f¨¢cilmente que se obtiene un flotador o toro pegando los lados rojos y azules. En la figura 5 pegamos los lados rojos y azules para obtener un flotador. No nos podemos olvidar de las circunferencias interiores verdes, que volvemos a dibujar en la figura 6. En la figura 7, tiramos de las circunferencias verdes hacia fuera para poder enfrentarlas y pegarlas. En la figura 8, deformando un poco m¨¢s la superficie y haci¨¦ndola m¨¢s homog¨¦nea, reconocemos perfectamente un flotador para dos.

Aunque solo ped¨ªamos la respuesta correcta, muchos lectores nos han enviado dibujos muy claros del proceso de construcci¨®n de la superficie. Aqu¨ª os dejamos los de Miguel ?ngel Ochando (ver imagen), Sergio Guerrero (ver imagen) y Javier Castellano Colmenero (ver imagen) para que cada cual busque el que m¨¢s le ayude a visualizar el resultado.

El razonamiento puede seguir otro orden o proponer otra manera distinta de visualizarlo. No hay que preocuparse siempre que se llegue al resultado: confiando en la demostraci¨®n de la clasificaci¨®n hecha por los matem¨¢ticos a principios del siglo XX, y que ya es todo un cl¨¢sico, sabemos que no importa el orden en que peguemos los lados.

Un comentario m¨¢s sobre el teorema de clasificaci¨®n citado. En realidad quiz¨¢s solo deformando no podamos llegar siempre a una de las superficies mencionadas, puede que aparezca como hecha un nudo en el espacio. Necesitaremos entonces cortar la superficie con unas tijeras y volver a pegar exactamente de la misma manera (si la superficie estuviera dibujada, al volver a pegar, el dibujo se recuperar¨ªa). Esto es muy distinto que romper la superficie, puesto que volvemos a pegarla de la misma manera. Por ejemplo, podemos construir un cilindro con una tira de papel pegando dos de sus lados. Pero tambi¨¦n podr¨ªamos pegar estos mismos lados de la misma manera -conservando el dibujo o, dicho de otro modo, el sentido de las flechas- pero dando una vuelta completa a la cinta antes de pegarla. Si deformando una superficie lleg¨¢ramos a este cilindro retorcido, cortando y volviendo a pegar obtendr¨ªamos el cilindro m¨¢s sencillo.

Algunos lectores han aludido a la botella de Klein. Esta es una superficie que no puede construirse en el espacio tridimensional sin cortarse o intersecarse a s¨ª misma, raz¨®n por la que deja de ser propiamente una superficie en el espacio. En particular no figura en la clasificaci¨®n dada (enunciada m¨¢s precisa en la versi¨®n escrita) que daba la pista sobre d¨®nde buscar la soluci¨®n.

Esperamos que todos hay¨¢is disfrutado con el desaf¨ªo topol¨®gico. El jueves plantearemos un nuevo reto.

Construyendo superficies

Un flotador biplaza