Desaf¨ªo criptogr¨¢fico: un misterio oculto en cuadraditos blancos y negros

Despu¨¦s de que Jordi entendiera en el desaf¨ªo anterior en qu¨¦ consist¨ªa el cifrado Vernam o One Time Pad, continu¨® con la videollamada con Paz, su madre.

¨DMam¨¢, lo de la criptograf¨ªa visual, ?qu¨¦ tiene que ver? Mi tutor, Paolo, insiste en que es m¨¢s o menos lo mismo que el Cifrado Vernam, pero no veo por d¨®nde va¡­

Paz sonre¨ªa ante la impaciencia de su hijo.

¡ªPues parte de la idea anterior, solo que aqu¨ª la informaci¨®n no est¨¢ codificada en forma de cadena binaria, sino como una imagen. Por tanto, no se tienen que hacer operaciones matem¨¢ticas para recuperar el secreto: se ocupa el ojo humano. Te mando unas fotos al m¨®vil.

¡ªIntenta superponerlas. S¨®lo tienes que imprimir en un papel un poco fino y las pones una encima de la otra en el vidrio de una ventana. Y obtendr¨¢s lo siguiente:

Ahora, f¨ªjate: si tomas la primera transparencia y la superpones con la que te mande a continuaci¨®n, ver¨¢s que obtienes una letra distinta. ?Cu¨¢l es?

Jordi pens¨® que mejor lo dejaba para m¨¢s tarde¡­ su madre segu¨ªa hablando, y no quer¨ªa perder el hilo.

¡ªPero hay algo m¨¢s ¡ªa?adi¨® Paz¡ª, la criptograf¨ªa visual a menudo incluye un ingrediente esencial para todo buen cript¨®grafo: la desconfianza.

¡ª??La desconfianza??

¡ªEso es. Si el emisor de un mensaje ni siquiera se f¨ªa del todo de un receptor concreto, puede repartir entre varios destinatarios la capacidad de descifrar. Para ello, la imagen que hace de clave va ¡°fragmentada¡± en varias transparencias: para recuperarla ser¨¢ necesario poner cuidadosamente las transparencias-clave una encima de la otra. Luego, situando esta ¡°pila¡± sobre la transparencia-mensaje, puede verse la imagen descifrada.

Jordi estaba intrigado.

¨DPero, ?c¨®mo se fabrican estas im¨¢genes a partir de la inicial?

¨DNo es dif¨ªcil. Para repartir un p¨ªxel negro de la imagen original deberemos elegir para cada una de las transparencias una de las dos combinaciones de p¨ªxeles siguiente:

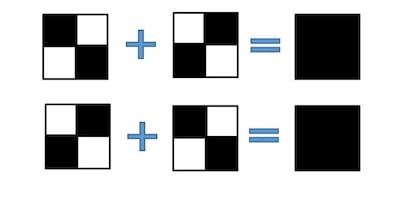
La elecci¨®n de una combinaci¨®n o de otra se tiene que hacer aleatoriamente. De la misma manera se hace para repartir un p¨ªxel blanco, usando eso s¨ª un material tal que al superponer dos transparencias negras se obtenga el color blanco (como eso no es f¨¢cil de reproducir en papel, que ser¨¢ el material que utilicen los lectores, jugaremos con los tonos de gris). As¨ª, para cada p¨ªxel original blanco debemos elegir aleatoriamente entre una de estas dos descomposiciones:

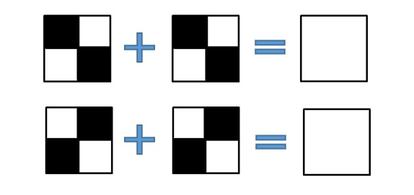
¨DPero es un trabajo pesad¨ªsimo¡­

¨DClaro: se tiene que implementar en programas que lo hagan r¨¢pidamente. La imagen original anterior tiene 100 p¨ªxeles. Pero, ?acaso alguien cifra a mano un mensaje para que viaje de forma segura por Internet? Ahora que ya lo entiendes, te planteo un nuevo desaf¨ªo: ?puedes jugar con estas transparencias a ver qu¨¦ imagen hay escondida y qu¨¦ combinaciones pueden recuperar la imagen secreta?

Paz colg¨®, pensando en que pod¨ªa incluso haberle planteado un reto m¨¢s exigente a Jordi; con el que quiz¨¢ se atreva alguno de nuestros lectores. ?Os anim¨¢is a enviarnos un mensaje cifrado con este m¨¦todo (y la clave asociada, para que podamos descifrar)? M¨¢s a¨²n, ?se os ocurre otro formato, no visual, por el que podamos implementar el Cifrado Vernam utilizando otro de nuestros sentidos? Nos encantar¨¢ ver vuestras propuestas, y comentaremos las mejores con la soluci¨®n de este reto.

Germ¨¢n S¨¢ez Moreno es investigador del grupo MAC y profesor de Matem¨¢tica Aplicada en la Universitat Polit¨¨cnica de Catalunya.

SOLUCI?N AL DESAF?O ANTERIOR

PRIMER EJERCICIO

La primera pregunta al lector del anterior desaf¨ªo era si podr¨ªamos obtener cualquier mensaje original probando claves distintas. Y la respuesta es que s¨ª, dado un cifrado, podemos hacer que ¡°encaje¡± con cualquier mensaje m enviado, fijando como clave la cadena c ? m, pues obviamente si a c le sumamos la cadena de bits c ? m obtendremos, de nuevo, el mensaje de partida, m. Esto ocurre por ser la operaci¨®n XOR autoinversa (y los dos ¡°c¡± cancelarse).

Para el ejemplo concreto propuesto, basta ver que

c?k¡¯= 01101 11010 00001 10101+01111 11010 00100 10001=00010 00000 00101 00100

es decir, obtenemos la palabra CAF?.

SEGUNDO EJERCICIO:

El segundo desaf¨ªo consist¨ªa en descifrar un mensaje oculto sabiendo que la clave era ¡°un testigo impagable de los tiempos¡±, y el mensaje original estaba relacionado con un dios del mar. Como pista adicional, ambos t¨¦rminos estaban relacionados con el lugar en el que se encontraba el protagonista del desaf¨ªo (Salerno, Italia).

Muchos lectores han encontrado la soluci¨®n y nos la han enviado a nuestro correo. A algunos, como a Efraim, Zoe y Gonzalo o Mariona, les ha ayudado conocer la zona; otros, como Luis, Ramiro o Manolo han probado posibles claves como Vesubio, Neptuno e incluso pizzero. La correcta, y la que se ajusta al ¡°testigo de los tiempos¡±, era POMPEYA que se codifica como:

K = 10000 01111 01100 10000 000100 11001 00000

Sumada a la cadena cifrada

C = 00000 01111 01000 00011 10000 01100 01100

Obtenemos el mensaje enviado:

10000 00000 00100 10011 10100 10101 01100

que se decodifica como PAESTUM (antigua ciudad de Poseidonia, en la provincia de Salerno).

En el enunciado hab¨ªa otra ¡°pista encubierta¡±, pues al ser la primera letra del cifrado 00000, necesariamente clave y mensaje enviado deb¨ªan ser palabras que empezasen por la misma letra. Pensamos que esta pista pod¨ªa ser ¨²til para reducir el chequeo de posibles claves; si uno utiliza ¡°Google/Wikipedia¡± y busca dos palabras de 7 letras relacionadas con Salerno y que empiecen por la misma letra, las opciones se reducen mucho ¡­.

Este desaf¨ªo se centra en el llamado Cifrado Vernam, propuesto a principios del Siglo XX por Gilbert S. Vernam, ingeniero de la compa?¨ªa telef¨®nica AT&T. Este m¨¦todo sirvi¨® de base para la definici¨®n por parte de Claude Shannon de la noci¨®n de cifrado perfecto. Rebautizado como One-time Pad, Shannon lo introdujo en su famoso trabajo ¡°Communication Theory of Secrecy Systems¡± Bell System Technical Journal 28(4) pp. 656¨C715, donde demostraba adem¨¢s que este m¨¦todo es seguro siempre que las claves sean de un solo uso y de la misma longitud que los textos a cifrar.

Puedes seguir a EL PA?S TECNOLOG?A en Facebook y Twitter o apuntarte aqu¨ª para recibir nuestra newsletter semanal.