La met¨¢fora del gin-tonic: ?qu¨¦ es un algoritmo cu¨¢ntico y por qu¨¦ son tan potentes?

Se nos dice que los computadores cu¨¢nticos ya est¨¢n aqu¨ª y que son mucho m¨¢s potentes que los convencionales. En particular, que en poco tiempo ser¨¢n capaces de romper nuestras claves criptogr¨¢ficas. Muchos pa¨ªses est¨¢n invirtiendo en esta tecnolog¨ªa para ser los primeros en alcanzar lo que se conoce como la ¡°supremac¨ªa cu¨¢ntica¡±. Pero, ?sabemos c¨®mo calcula un computador cu¨¢ntico y cu¨¢l es la raz¨®n de esa potencia que se les atribuye?

Empecemos por la memoria. En un ordenador tradicional su unidad m¨ªnima es el bit, que puede contener un 0 o un 1. En un ordenador cu¨¢ntico es el c¨²bit ¡ªabreviatura de bit cu¨¢ntico¡ª que puede contener un 0 o un 1, pero tambi¨¦n cualquier combinaci¨®n de esos dos estados b¨¢sicos. Los f¨ªsicos llaman a esta caracter¨ªstica ¡°superposici¨®n de estados¡± y nos dicen que eso es lo normal en el mundo de lo muy peque?o. Una part¨ªcula ¡ªtal como un prot¨®n¡ª tiene, por ejemplo, una propiedad llamada ¡°esp¨ªn¡±, relacionada con sus propiedades magn¨¦ticas, que puede adoptar dos valores b¨¢sicos llamados ¡°arriba¡± y ¡°abajo¡±, aunque lo habitual es que su estado sea una combinaci¨®n de ambos. Podemos poner como analog¨ªa mundana de esta superposici¨®n un gin-tonic, el cual tendr¨¢ una cierta proporci¨®n de ginebra y otra de t¨®nica. La informaci¨®n relevante que almacena el c¨²bit es el par de proporciones a y b de cada estado, es decir, dos n¨²meros (para mayor precisi¨®n, se trata adem¨¢s de dos n¨²meros complejos). Esto nos da ya una idea de la potencia de almacenamiento de un c¨²bit (cualquier proporci¨®n de ginebra y t¨®nica) con respecto a la de un bit tradicional (solo ginebra, o solo t¨®nica).

Otra caracter¨ªstica del mundo f¨ªsico es que los estados de dos part¨ªculas cu¨¢nticas pueden estar entrelazados, entendiendo por ello que est¨¢n ligados entre s¨ª. Esto nos permite construir memorias con varios c¨²bits entrelazados. De esa forma, dos c¨²bits estar¨ªan en una superposici¨®n de los cuatro estados b¨¢sicos 00, 01, 10 y 11. Como consecuencia, dos c¨²bits almacenan cuatro n¨²meros y, en general, n c¨²bits entrelazados almacenan 2¦«n (2 elevado a n) n¨²meros. Por ejemplo, en cinco bits las memorias tradicionales almacenan un solo n¨²mero entero entre el 0 y el 31, pero cinco c¨²bits entrelazados almacenan 32 n¨²meros complejos. Y ah¨ª hay una ganancia exponencial.

Vayamos ahora con el c¨®mputo: los c¨²bits operan entre s¨ª mediante las llamadas ¡°puertas cu¨¢nticas¡±. Por ejemplo, existe una puerta llamada X que, aplicada a un c¨²bit, convierte un 0 en un 1 y un 1 en un 0. Pero, esa puerta X es algo m¨¢s compleja: aplicada a un c¨²bit con proporciones a y b de 0 y 1, pasa a un estado con proporciones b y a de 0 y 1. En nuestra analog¨ªa del gin-tonic, la puerta X intercambiar¨ªa las cantidades de ginebra y de t¨®nica.

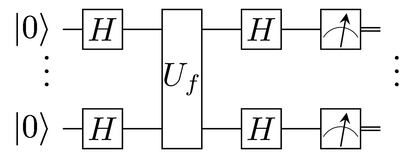
Al igual que hacemos con los circuitos de los ordenadores convencionales, enlazando varias puertas cu¨¢nticas se puede calcular una funci¨®n compleja. Un algoritmo cu¨¢ntico es, en esencia, un circuito formado por puertas cu¨¢nticas, que transforma el estado de un conjunto de c¨²bits desde una superposici¨®n inicial hasta otra final. ?De d¨®nde procede entonces su supuesta mayor potencia de c¨¢lculo?

Imaginemos una funci¨®n implementada con puertas cu¨¢nticas, como, por ejemplo, la ra¨ªz cuadrada entera de un n¨²mero. Supongamos que bastan n c¨²bits para contener el n¨²mero de entrada. Mediante puertas cu¨¢nticas, es f¨¢cil conseguir que los n c¨²bits alcancen un estado que sea una superposici¨®n de todos los estados posibles de n bits. Siguiendo el ejemplo anterior, con cinco c¨²bits alcanzar¨ªamos una superposici¨®n de 32 estados. Aqu¨ª es donde aparece la mayor potencia de los computadores cu¨¢nticos: el circuito cu¨¢ntico calcular¨ªa la ra¨ªz cuadrada a la vez para los 32 valores posibles de la entrada y dejar¨ªa las 32 ra¨ªces cuadradas como una superposici¨®n en los c¨²bits de salida. Es decir, puede hacer en un solo paso lo que al ordenador convencional le costar¨ªa hasta 32 pasos realizar.

Pero, no todo es de color de rosa en el mundo cu¨¢ntico porque este tiene algunos ¡°caprichos¡±: las proporciones de la superposici¨®n ¡ªla proporci¨®n de ginebra y t¨®nica¡ª pertenecen a la ¡°vida ¨ªntima¡± de las part¨ªculas cu¨¢nticas. Si un observador intenta medir el estado de los c¨²bits, su superposici¨®n se destruye. Es lo que sucede en la realidad f¨ªsica, aunque nadie sabe por qu¨¦: si se mide el esp¨ªn de un prot¨®n, se destruye la superposici¨®n y el observador obtendr¨¢ uno de los dos estados, ¡°arriba¡± o ¡°abajo¡±, con cierta probabilidad cada uno, dependiendo de los valores de a y b. Es como si, al bebernos nuestro gin-tonic, se destruyera la mezcla que contiene y bebi¨¦ramos s¨®lo ginebra o s¨®lo t¨®nica, sin poder anticipar cu¨¢l de las dos vamos a beber.

Los algoritmos cu¨¢nticos necesitan del ingenio humano para conseguir extraer m¨¢s informaci¨®n a partir de la superposici¨®n de salida. Una forma habitual de proceder es hacer interferir los resultados calculados, unos con otros, mediante puertas cu¨¢nticas adicionales. Por ejemplo, podr¨ªamos calcular la suma o el producto de todos ellos o bien determinar cu¨¢ntos de ellos son pares y cu¨¢ntos impares. El m¨¢s famoso de los algoritmos cu¨¢nticos, el que descompone un n¨²mero entero en sus factores primos ¡ªdebido al matem¨¢tico Peter Shor, en 1994¡ª, utiliza t¨¦cnicas de este tipo.

Los algoritmos cu¨¢nticos ya est¨¢n aqu¨ª. Ahora solo necesitamos computadores cu¨¢nticos con cientos de c¨²bits para ejecutarlos.

Ricardo Pe?a Mar¨ª es Catedr¨¢tico Em¨¦rito de Lenguajes y Sistemas Inform¨¢ticos de la Universidad Complutense de Madrid

Cr¨®nicas del Intangible es un espacio de divulgaci¨®n sobre las ciencias de la computaci¨®n, coordinado por la sociedad acad¨¦mica SISTEDES (Sociedad de Ingenier¨ªa de Software y de Tecnolog¨ªas de Desarrollo de Software). El intangible es la parte no material de los sistemas inform¨¢ticos (es decir, el software), y aqu¨ª se relatan su historia y su devenir. Los autores son profesores de las universidades espa?olas, coordinados por Ricardo Pe?a Mar¨ª (catedr¨¢tico de la Universidad Complutense de Madrid) y Macario Polo Usaola (profesor titular de la Universidad de Castilla-La Mancha).

Para consultar las cr¨®nicas de otros a?os, haga clic aqu¨ª.

Puedes seguir a EL PA?S TECNOLOG?A en Facebook y Twitter o apuntarte aqu¨ª para recibir nuestra newsletter semanal.